بازدیدکننده گرامی باسلام. بدلیل حجیم بودن پیوستهای ب و پ این دو با صفحه اصلی لود نشده واز فهرست جدولی سمت راست صفحه قابل دسترسی هستند. همچنین با انتخاب گزینه "همه صفحات" کل متن به اضافه ضمائم قابل دسترسی هستند.

 

 

 

 

 

 

 

بسمه تعالی

بررسی و شبیه سازی سیستمهای حذف فعال نویز

با تشکر از اساتید گرامی جناب آقای دکتر محمد بهدادفر ( این آدرس ایمیل توسط spambots حفاظت می شود. برای دیدن شما نیاز به جاوا اسکریپت دارید ) و جناب آقای مهندس محمدابراهیم صادقی ( این آدرس ایمیل توسط spambots حفاظت می شود. برای دیدن شما نیاز به جاوا اسکریپت دارید )

 

فاطمه صالحی - این آدرس ایمیل توسط spambots حفاظت می شود. برای دیدن شما نیاز به جاوا اسکریپت دارید

 فصل اول : مقدمه

فصل اول : مقدمه

 1-1 کلیات

یکی از روشهای نوین حذف نویز صوتی،روش حذف فعال نویز است. ازآنجا که پیاده سازی این روش مستلزم استفاده از سیستمهای پردازش سیگنال است و روشهای مختلفی برای پردازش سیگنال وجود دارد،آگاهی از عملکرد هرکدام از این روشها با توجه به خصوصیات نویز وامکانات سخت افزاری در دسترس، ما را در انتخاب روش مناسب یاری خواهد نمود.در این نوشتار سعی براین است که با بررسی تعدادی از الگوریتمهای مرسوم مورد استفاده درفیلترهای وفقی در روش حذف فعال نویز و معرفی تعدادی روشهای بکار رفته برای ترکیب بندیهای مختلف سیستم حذف فعال نویز به یک دیدگاه کلی در مورد این سیستمها دست یابیم. در فصل دوم به بررسی انواع ترکیب بندیهای مرسوم مورد استفاده در روش حذف فعال نویز و الگوریتمهای وفقی مورد استفاده در آنها خواهیم پرداخت. در فصل سوم با استفاده از نرم افزار MATLAB،تعدادی از الگوریتمهای فیلتر وفقی شبیه سازی شده است. در قسمت ضمیمه، به عنوان مثال کاربردی استفاده از سیستم حذف فعال نویز، کاردیوگرافی قلب جنین و نمونه برداری از ضربان قلب جنین شبیه سازی شده است.

2-1 اهداف

ازآنجا که سیستم حذف فعال نویز بر مبنای پردازش سیگنال می باشد،یکی از شرایط تاثیر گذار بر روی انتخاب الگوریتم پردازشی،سخت افزارمورد استفاده است.روش حذف فعال نویز ،بیشترین بازده را در فرکانسهای پایین (زیر 500Hz) داراست.ایده اصلی روش حذف فعال نویز (Active Noise Control) تولید صوتی با فاز مخالف می باشد که مجموع این سیگنال و سیگنال نویز،باعث کاهش دامنه نویز خواهد شد. روش فعال حذف نویز، کارایی خود را در فرکانسهای بالاتر از 500Hz بتدریج از دست می دهد زیرا نیاز به پردازش سنگین خواهد بود. روش حذف فعال نویز ترکیبی از علوم مهندسی آکوستیک، الکترونیک وپردازش سیگنال است. برای عملی نمودن روش حذف فعال نویز لازم است در ابتدا محدودیتها وامکانات  در دسترس شناسایی شود تا با استفاده از آنها بتوان این روش را پیاده سازی نمود. ایده اولیه این طرح در سال 1930 مطرح گردید. با اینحال بدلیل نبود امکانات فنی تاسال 1990 مسکوت گذاشته شد. در سالهای اخیربا گسترش وتوسعه سیستمهای پردازش سیگنال وپیشرفت ابزارهای محاسباتی استفاده از این سیستم ممکن شده است. با اینحال انتخاب بین الگوریتمهای مختلف موجود بسته به خصوصیات نویز و محیط انتشار و امکانات سیستم پردازشی قدم اول در استفاده از این سیستم است.

3-1 فرضیات

فرض بر این است که نویز حذف شونده از نوع پخشا می باشد.یعنی انرژی نویز در تمام نقاط محیط مورد نظر یکسان است.همچنین از تاثیر عوامل غیر خطی صرفنظر شده است.

 4-1 تعریف مفاهیم

 سیستم کنترل فعال نویز

اساس یک سیستم حذف فعال نویز در شکل1-1 توضیح داده شده است. هر سیستم متشکل از دو قسمت الکترونیکی وآکوستیکی است. آنچه که یک سیستم حذف فعال نویز انجام می دهد،در واقع افزودن سیگنالی با فاز مخالف به سیگنال اولیه است.

                                                 

                                             

در فرمول1-1اندیس P برای ¹SPL سیگنال اولیه واندیس S برای SPL سیگنال تولید شده از سیستم استفاده شده است.جمع SPL دو سیگنال است.

 

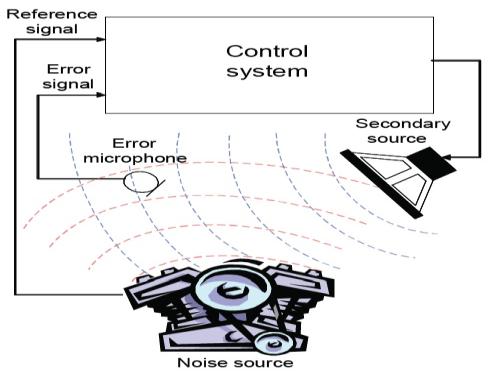
شکل (1-1) شمای کلی یک سیستم حذف فعال نویز

 

سیستم کنترل از یک سیگنال نمونه که از روی سیگنال نویز ساخته شده است،بعنوان مرجع استفاده می نماید.سیگنال دیگر مورد استفاده سیستم،سیگنال خطا است که درواقع باقیمانده نویز حاصل جمع سیگنالهای S و P است.سیستمی که تنها از سیگنال نویز جهت ساختن سیگنال ضد نویز استفاده می کند،پس خور2 و سیستمی که از سیگنال خطا برای تولید سیگنال  P استفاده مینماید،سیستم دارای پیش خور³ نامیده می شود.علاوه براین سیستم کنترل فعال نویزدارای دسته بندی دیگری بصورت سیستم باند باریک وپهن باند است که نوع آن وابسته به سیگنال نویز است.سیستم باند باریک غالبا تحت نام سیستم تونال ⁴شناخته می شود.خروجی سیستم به بلندگوها یا مبدلهای آنتی نویز انتقال می یابد.با در نظر گرفتن این نکته که سیگنال نویز سیگنال اولیه است،این مبدل ها به عنوان منابع ثانویه مولد صوت در سیستم محسوب می شوند.این مبدلها معمولاًبلندگوهای دینامیکی هستند ولی از انواع دیگرمانند مبدلهای پیزوالکتریک می توان استفاده نمود که با اتصال به صفحه غالبا فلزی می توانند درحذف انواع خاصی از نویز موثر باشند.

 

---

 1Sound Pressure Level

2 Feed Forward

3 Feedback

4 Tonal Feedforward Control System

فیلتر وفقی (Adaptive Filter)

          درون یک سیستم کنترل فعال نویز،فیلتری وجود دارد که نمودار بلوکی آن در شکل 2-1 نمایش داده شده است.این فیلتر خود را به گونه ای تنظیم می کند که سیگنال مرجع ورودی را فیلتر نموده و خروجی آن با الگوی نویز اولیه مطابقت نماید.در واقع فیلتر از دو قسمت مجزا شامل خود فیلتر و الگوریتم وفقی تشکیل است که دائما درحال تنظیم فیلتر است.دراکثر مواقع از فیلترهای (FIR) که دارای پاسخ ضربه محدود می باشند استفاده می شود.راه حل دوم استفاده از فیلترهای با پاسخ ضربه بینهایت (IIR) است.این فیلترها قادرند الگوریتمهای پیچیده را پیاده سازی نموده وبا طراحی یک پیش خور مناسب همانند فیلترهای FIR عمل نمایند.یک جنبه منفی آن این است که خروجی یک فیلتر IIR ممکن است به جای مینیمم مطلق به یک مقدار مینیمم همگرا شود.همچنین ممکن است رسیدن به این مقدار مطلوب روندی کند وبی ثبات داشته باشد.

 

 

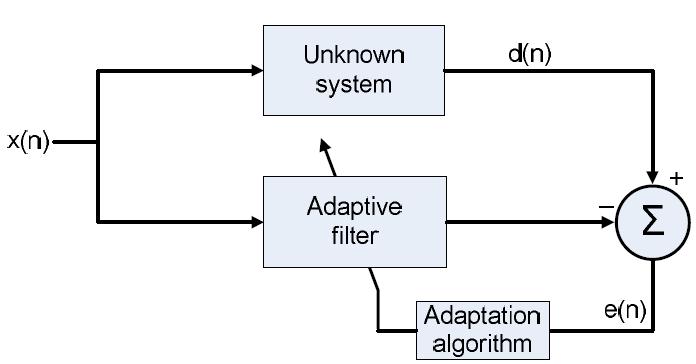
شکل (2-1) شمای یک فیلتر وفقی . x(n) سیگنال مرجع ورودی ،d(n) سیگنال مطلوب و e(n) سیگنال خطا است .

 

می توان مقدار بهینه ضرایب  فیلتر FIR را برای نویزساکن بااستفاده ازمقدار همبستگی بین سیگنالهای مطلوب d(n)و مرجعx(n) در شکل2-1و خودهمبستگی با سیگنال مرجع محاسبه نمود.ضرایب بهینه،میانگین مربعات خطا را مینیمم می کنند.بنابراین در کاربردهای عملی و بدون نویزثابت،امکان محاسبه ضرایب بهینه فیلتر با استفاده از خصوصیات همبستگی سیگنالهای ورودی وجود ندارد.از آنجا که ضرایب فیلتر بایستی دایما محاسبه شوند،بار محاسباتی سنگینی بر سیستم وارد خواهد شد. ضرایب w فیلتر طبق فرمول گرادیانی زیربازیابی می شوند تا جایی که مقدار بهینه بدست آید.                                                                                             

1-1

در فرمول 1-1، n اندیس تکرار،µ فاکتور همگرایی ویا مقدارپله،گرادیان میانگین مربع خطا است. میانگین مربع خطا از رابطه زیر بدست می آید:

   1-2

E[] عملگرمقدار امید ریاضی وe(n)سیگنال خطا است.استفاده از الگوریتم کاهش پله ای¹،برای تخمین گرادیان سطح میانگین مربعی حداقل²LMS نامیده می شود.در این روش مقدار میانگین مربعی خطا با مقدار لحظه ای خطا تخمین زده می شود.گرادیان مورد نظر می تواند با معادله  تخمین زده شود که سیگنال خطا e(n) از رابطه زیربدست می آید.

1-3      

d(n) سیگنال مطلوب و x(n) سیگنال مرجع است.بدون در نظر گرفتن محاسبات برداری،گرادیان تخمینی برای هر مقدار w جدید فیلتر وفقی از محاسبه و جمع با مقدار قبلی طبق فرمول زیر بدست می آید:

  1-4   

l پله فیلترو µ فاکتور همگرایی نامیده می شود.با دردست داشتن مقدار فاکتور همگرایی می توان سرعت همگرایی را در الگوریتم فیلتر تنظیم نمود.درصورتیکه فاکتور همگرایی خیلی بزرگ باشد،فرآیند تولید ضرایب فیلتر ناپایدار خواهد شد.درصورتیکه فاکتور همگرایی خیلی کوچک باشد،فرآیند تولید ضرایب بی نتیجه خواهد بود.شاخص محدوده فاکتور همگرایی از رابطه زیر بدست می آید:[50].

1- 5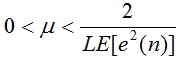      

که  Lطول فیلتر است.

 

---

1Steepest Decent Algorithm

2Least Mean Square

 فصل دوم : مبانی نظری

 1-2 بررسی تحقیقات پیشین

 1-1-2 کنترل پس خور

باتوجه به آنچه که در بخش1-1گفته شد،سیستم پس خور سیستمی است که تنها ورودی سیگنال مرجع را دارا است.با این تعریف سیستم دارای پیش خور وپس خور از هم مجزا می شوند.اصولا در سیستم کنترل پس خور،زمانی که طول می کشد تا نویز ازمکان آشکارسازی سیگنال مرجع به سنسورخطا برسد،بایستی بزرگتر از زمانی باشد که سیستم الکترونیکی وکنترلی نیاز دارد تا سیگنال در فاز مخالف درهمان مکان راتولید نماید.اگر نویز تک فرکانس باشد،و مشخصات نویز به کندی تغییر نماید،حالت گفته شده می تواند نادیده گرفته شود.تنها محدودیت موجود در این حالت که بایستی درنظرگرفته شود،مربوط به سرعت تغییر دامنه وفرکانس نویز است.تقریبا تمامی سیستمهای کنترل نویز پس خور دیجیتالی هستند[51] که این بدلیل ماهیت پردازشی سیستمهای حذف فعال نویز است.

 

2-1-2 ANC پهن باند پس خور

این سیستم ها دارای یک منبع ثانویه،یک سنسور مرجع،و یک سنسور خطا می باشند.سیستم آکوستیکی تک کانال ANC که در شکل1-2 نشان داده شده است،نمونه ای از این سیستم ها است.

 

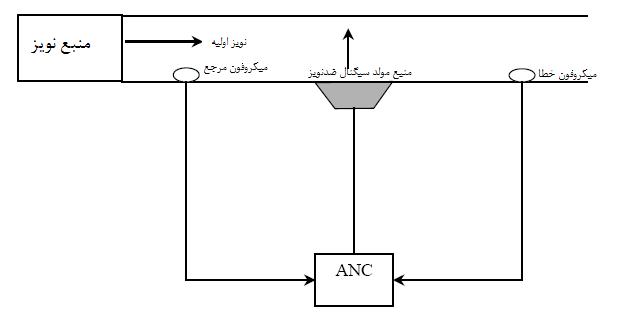
شکل(1-2) حذف فعال نویزپهن باند به روش پس خور تک کاناله

 

این سیستم ابتدایی ANC پهن باند را می توان به عنوان یک چارچوب شناسایی سیستم وفقی در نظر گرفت.در اصل،از یک فیلتر وفقی W(z) برای تخمین یک پروسه نامعلوم P(z) که شامل پاسخ آکوستیکی از سنسور مرجع به سنسور خطا است،استفاده می شود.هدف فیلتر وفقی W(z)،مینیمم کردن سیگنال خطای باقیمانده است.تفاوت اصلی این طرح با سیستم های الکترونیکی،استفاده ازیک  گره جمع کننده آکوستیکی به جای جمع کننده سیگنال های الکترونیکی است.بنابراین تنظیم و جبران سازی تابع انتقال مسیر ثانویه S(z) از خروجی فیلتر وفقی تا نقطه ثبت سیگنال خطا،ضرورت دارد.   

 

 

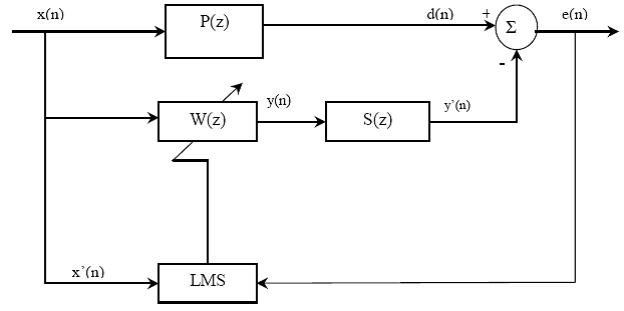
شکل (2-2) شمای کلی یک سیستم حذف فعال نویز

 

با توجه به شکل 2-2 می بینیم که تبدیل z سیگنال خطا به صورت زیر خواهد بود:

2-1   

با فرض صفر شدن سیگنال خطا پس از همگرایی فیلتر وفقی،W(z) باید تابع انتقال بهینه را بدست آورد.

2-2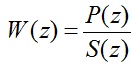        

ایجاد تابع انتقال مسیر ثانویه در یک سیستم با استفاده از الگوریتم استاندارد LMS،منجر به ناپایداری می شود.علت این امر این است که امکان جبران سازی تاخیر ذاتی ناشی از S(z)،در صورتی که با تاخیر مسیر اولیه P(z) یکسان نباشد،وجود ندارد.همچنین برای مدل سازی موثر 1/S(z)،به یک فیلتر FIR بسیار بزرگ نیاز داریم.این مشکل را می توان با قرار دادن یک فیلتر مشابه در مسیر آپدیت وزن های معادله LMS سیگنال مرجع،حل کرد که آن را به نام الگوریتم FX-LMS¹ می شناسیم [5][6]. بلوک دیاگرام یک سیستم ANC با استفاده از الگوریتم FXLMS در شکل 3-2 نشان داده شده است. تعریف ابتدایی الگوریتم FXLMS در ادامه بیان می شود.

 

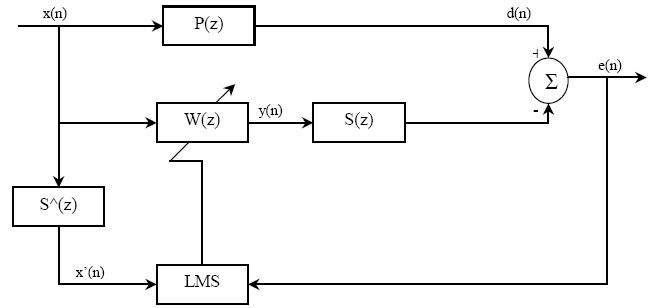
شکل (3-2) سیستم حذف فعال نویز با استفاده از الگوریتم FXLMS

در شکل 3-2 سیگنال خطای باقیمانده را می توان به صورت زیر بیان کرد:

2-3    

که در آن s(n) برابر پاسخ ضربه مسیر ثانویه S(z) در زمان n می باشد.با در نظر گرفتن تابع هزینه میانگین مربعات ،فیلتر وفقی می تواند مربع خطای لحظه ای  را به صورت زیر مینیمم کند:

                        2-4      

چون

                             2-5    

در نتیجه معادله اصلاح وزن به صورت زیر خلاصه می شود:

          2-6   

 در کاربرد های عملی،تابع انتقال مسیر ثانویه S(z) نامعلوم است و باید بوسیله یک فیلتر اضافی تخمین زده شود.بنایراین اگربرابر پاسخ ضربه باشد،داریم . الگوریتم FXLMS نسبت به خطاهای موجود در تخمین S(z)‌ بوسیله فیلتر،مقاومت خوبی از خود نشان می دهد و با وجود کندی همگرایی،این الگوریتم به همگرایی در حدود 90 درجه خطای فاز بین S(z)‌ و  دست می باید (Morgan [7] ). بنابراین می توان از تکنیک های مدل سازی آفلاین برای مدل سازی S(z) استفاده کرد [3].Nelson and Elliot [8] نشان می دهند که ماکزیمم اندازه گام قابل استفاده با الگوریتم FXLMS برابر است با:

2-7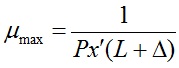    

که در آن  برابر توان سیگنال مرجع فیلتر شده و Δ برابر تعداد نمونه های مطابق با تاخیر کلی در مسیر ثانویه است.البته خطاهای موجود در تخمین تابع انتقال مسیر ثانویه،باعث تغییر محدوده پایداری نسبت به µ می شود [9]. تحلیل دقیق مقیاس پایداری را می توانید در مقاله [10] بیابید.

در سیستم ANC پس خور نشان داده شده در شکل 2-2،خروجی آنتی نویز نیز به بالادست میکروفون مرجع می تابد که منجر به پیش خور آکوستیکی و در نتیجه یک سیگنال مرجع خراب x(n) میشود.اگر تاخیر فاز حلقه باز به 180 درجه برسد ( پس فاز ) و بهره بزرگتر از یک باشد،ناپایداری رخ می دهد.این مساله را می توان با استفاده از یک فیلتر وفقی آفلاین حذف پیش خور مجزا² در سیستم ANC،حل نمود.همچنین می توان پیش خور را با استفاده از یک فیلتر وفقی IIR به جای فیلتر FIR در سیستم ANC‌ حل کرد.البته فیلتر های IIR دارای پایداری مطلق بی قید و شرط نیستند چون فرآیند انطباق ممکن است به یک مینیمم محلی همگرا شده و همچنین ممکن است سرعت همگرایی آن نسبتا کند باشد.آنالیز کامل و دقیق فیلتر های وفقی IIR‌ در مقاله [11] قابل دسترسی است.

 

 

 

---

1Filtered-X LMS

2separate offline adaptive feedback cancellation filter

 

 

3-1-2 ANC پس خور باند باریک

منابع نویز زیادی به صورت پریودیک در طبیعت وجود دارند ( مانند موتور ها،کمپرسور ها،ماشین ها ،پنکه ها،و غیره).در این موارد برای تامین یک سیگنال مرجع الکتریکی که شامل فرکانس اولیه و کلیه هارمونیک های نویز تولید شده باشد،از روش مشاهده مستقیم حرکت مکانیکی با استفاده از یک سنسور مناسب استفاده می شود.بلوک دیاگرام ابتدایی در شکل 4-2 نشان داده شده است.

 

 

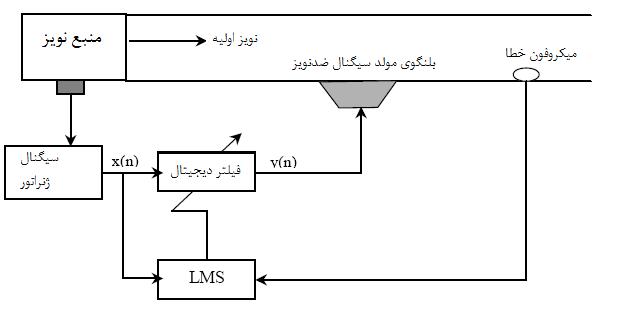
شکل (4-2)  سیستم ANC باندباریک بون پیش خور

 

این تکنیک از پیش خور آکوستیکی نامطلوب به سنسور مرجع و همچنین از مسایل مربوط به کهنگی و غیر خطی بودن میکروفون های آکوستیکی،جلوگیری می کند.متناوب بودن نویز باعث حذف محدودیت علی بودن می شود چون هر هارمونیک را می توان به صورت مستقل کنترل کرده و برای مدل سازی مسیر ثانویه می توان از فیلتر FIR کوچک تری استفاده کرد.دو تکنیک برای ANC باند باریک وجود دارد که عبارتند از:

روش اول تکنیک ترکیب و سنتز شکل موج که در آن از یک قطار ضربه با دوره تناوب برابر با عکس بسامد اصلی پارازیت و اغتشاش،استفاده می شود.تکنیک دوم از یک فیلتر وفقی باندنگذر تیز¹ با یک سیگنال مرجع سینوسی استفاده می کند.

 

---

1Notch

 

4-1-2 ANC با پیش خور

سیستم های ANC پس خور (باند باریک یا پهن باند)،از یک سنسور مرجع (که سیگنال نویز اولیه را اندازه گیری می کند) و از یک فیلتر وفقی پس خور و یک سنسور خطا برای اندازه گیری نویز باقیمانده تشکیل شده اند.البته در برخی موارد،داشتن یک سنسور برای اندازه گیری یا تولید داخلی سیگنال خطا،امکان پذیر نمی باشد.در این بخش الگوریتم ANC پیش خور دار را توصیف می کنیم که در آن سیگنال مرجع از خروجی سنسور خطا تولید شده است.کاربرد این روش در مواردی است که نویز از اغتشاش تولید شده باشد.بطورمثال نویز از منابع متعددی تولید شده و مسیر انتشار باعث ایجادتشدید در مکانهایی از فضای انتشار شود.دراینصورت هیچ سیگنال مرجعی در دسترس نمی باشد زیرا مکان سنسورها قابل تشخیص نیست.

5-1-2 ANC باپیش خورو غیر وفقی

اولین ارایه سیستم ANC با پیش خورغیر وفقی توسط Olson and May [4] انجام شد که از یک تقویت کننده استفاده می کرد که به صورت دقیقی با پاسخ سنسور خطا و منبع ثانویه،انطباق یافته بود. Hong and Eghtesadi [12] درباره کاربرد های ANC با پیش خور برای کاهش نویز درون یک کانال، مطالعاتی انجام دادند.Veit [13], Carme [14] and Wheeler [15] درباره موارد کاربرد ANC باپیش خور برای حذف نویز مطالعه کرده اند.بلوک دیاگرام یک سیستم ANC پیش خور دار کلاسیک در شکل 5-2 نشان داده شده است.

 

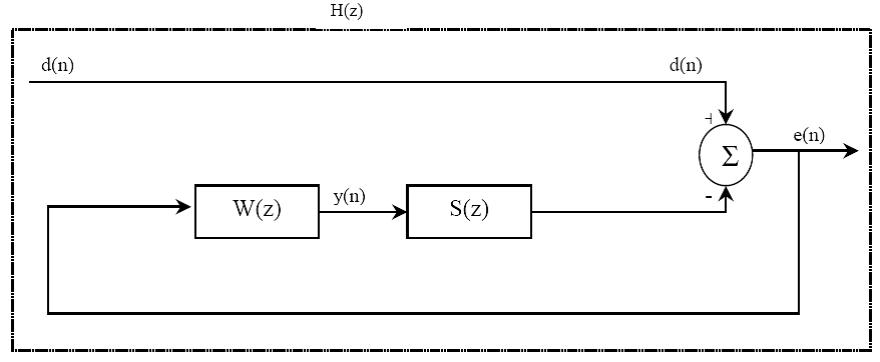
شکل (5-2) بلوک دیاگرام یک سیستم ANC پیش خور دار کلاسیک

در شکل 5-2 d(n) برابر نویز اولیه در محل سنسور خطا،e(n) نویز باقیمانده،y(n)‌ سیگنال آنتی نویز یا سیگنال ثانویه،W(z) تابع انتقال کنترل کننده،و S(z) تابع انتقال مسیر ثانویه می باشد.در شرایط حالت پایدار،تبدیل z سیگنال خطا به صورت زیر بیان می شود:

 

2-8  

          2-9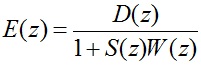                

بنابراین تابع انتقال حلقه بسته H(z) از نویز اولیه تا سیگنال خطا به صورت زیر است:

    2-10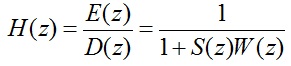   

با توجه به رابطه 2-9 طیف توانی سیگنال خطا برابر است با:

2-11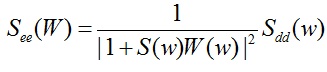   

 

 

كه در آن See(w) و Sdd(w) به ترتيب برابر طيف تواني سيگنال خطا (e(n)) و نويز مرجع (d(n)) مي باشند.بنابراين براي مينيمم كردن S_ee(w) ،يا بايد مقدار  مينيمم شود و يا بهره S(z)W(z) به بينهايت برسد.اگر پاسخ فركانسي S(w) به صورت تخت باشد،آنگاه بهره W(w) مي تواند بدون هيچ محدوديتـي افزايش يابد.البته اين مورد به ندرت رخ مي دهد كه پاسخ مسير ثانويه باعث شيفت فاز قابل ملاحظه اي شود.از خروجي فيلتر كنترل تا سنسور خطا،مقداري تاخير انتشار وجود دارد.اين تاثيرات باعث بوجود آمدن شيفت فاز در S(w) شده كه با فركانس افزايش مي يابد. با رسيدن شيفت فاز به 180 درجه،فيدبك منفي مطلوب به فيدبك مثبت تبديل شده و به ناپايداري منجر ميشود.بنابراين با افزايش شيفت فاز و فركانس،بهره W(w) بايد كاهش يابد.بنابراین طراحي يك فيلتر معكوس كننده،به صورتي كه بهره آن آنقدر بزرگ نباشد كه وقتي شيفت فاز برابر 180 درجه است بهره حلقه شبكه از مقدار يك واحد بزرگتر شود،نتیجه می شود. پس اگر:

                                                            2-12                                                       

2-13                    

و با داشتن مسير ثانويه S(w)،W(w) بايد به گونه اي انتخاب شود كه وقتي  است بهره G(w) ماكزيمم شود.جزييات بيشتري درباره طراحي سيستم ANC فيدبك  دار در مقالات و نوشته هاي [3][13][14] قابل دسترسي است.

6-1-2 ANC با فيدبك تك كانال وفقي

اين سيستم براي نخستين بار توسط Eriksson[16] ارايه شده و توسط Popovich [17][18] به صورت چند كاناله توسعه يافت.اين تكنيك معمولا به عنوان يك سيستم ANC فیدبك دار وفقي شناخته مي شود كه واقعا سيگنال مرجع خود را سنتز (تركيب) مي كند.همچنين  مي توان تحت شرايط خاصي،سيستم را به عنوان پيش بيني كننده وفقي در نظر گرفت [19].

در سيستم ANC فيدبك دار نشان داده شده در شكل 6-2،سيگنال نويز اوليه d(n) در دسترس نميباشد.بنابراين مهم ترين مساله سيستم ANC وفقي فيدبك دار اين است كه مجددا سيگنال مرجع d(n) را از روي سيگنال خطا بسازد.با توجه به شكل 6-2 درمي يابيم كه نويز اوليه به صورت زير بيان مي شود.

                                                2-14                                                            

كه E(z) برابر سيگنال خطاي باقيمانده بدست آمده از سيگنال خطا است و Y(z) برابر خروجي فيلتر وفقي مي باشد.تابع انتقال مسير ثانويه S(z) نيز با  تقريب زده مي شود. در نتيجه مي توانيم نويز اوليه d(n) را تخمين زده و از آن به عنوان سيگنال مرجع ترکیبی x(n) به صورت زير استفاده كنيم.

 

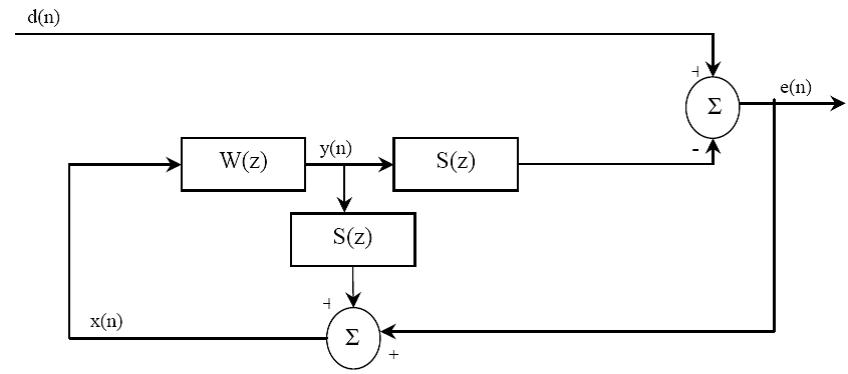
شکل (6-2)  سیستم ANC با فیلتر وفقی پیش خور دار که در آن از سیگنال مرجع ترکیبی استفاده شده است.

 

            2-15           

                       

بلوك دياگرام یک سيستم ANC پهن باند نمونه در شكل 7-2 نشان داده شده است.

 

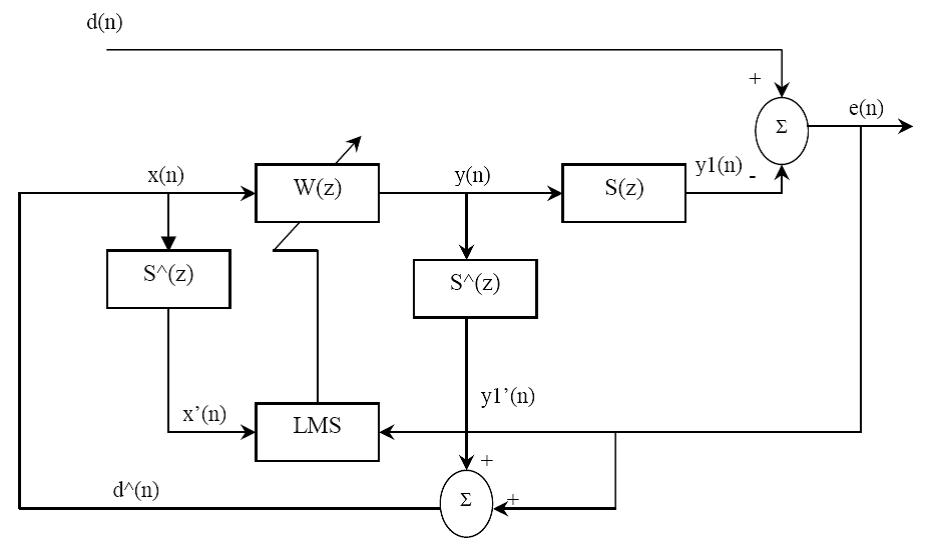
شکل (7-2)  سيستم ANC پهن باند پیش خور داربا استفاده از الگوریتم FXLMS

 

با توجه به اين شكل مي بينيم كه سيگنال مرجع x(n) كه از سيگنال خطا سنتز شده است،به صورت زير بيان مي شود:

                        2-16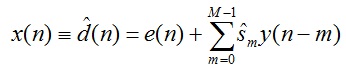       

كه  برابر M امين درجه فيلتر FIR () استفاده شده در تخمين تابع انتقال مسير ثانويه است.اين تخمين يا به صورت آنلاين و يا به صورت آفلاين قابل اجرا است. سيگنال ثانويه به شكل زير ساخته شده است.

                                            2-17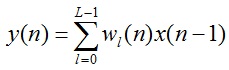      

كه  برابر ضرايب L امين مرتبه فيلتر FIR وفقي W(z) در زمان n است. اين ضرايب بوسيله الگوريتم LMS به صورت زير اصلاح مي شوند.

                     2-18      

كه µ برابر اندازه گام ( step ) و سيگنال مرجع فيلتر شده  برابر است با:

                                             2-19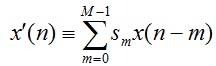              

با توجه به معادلات 2-14 و 2-15 مي بينيم كه (x(n)=d(n  اگر(s(z= .با فرض وجود اين شرايط،سيستم ANC‌ فيدبك دار وفقي شكل 7-2 را ميتوان به سيستم ANC بدون فيدبك شكل3-2 تبديل كرد.اگر الگوريتم LMS داراي سرعت همگرايي كند باشد( يعني اندازه گام µ كوچك باشد [5] ) آنگاه فيلتر وفقي W(z) را مي توان بوسيله تابع انتقال مسير ثانويه S(z) محاسبه نمود.به علاوه اگر فرض كنيم كه مسير ثانويه S(z) را بتوان به صورت يك تاخير خالص مدل سازي كرد(يعني)آنگاه سيستمANC‌ فيدبك دارمعادل دستگاه پيش بين وفقي¹ استاندارد شكل 8- 2 مي باشد.

 

 

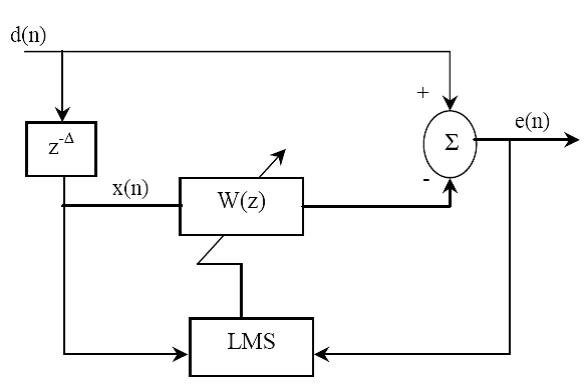
شکل (8-2)  الگوریتم ANC با پیش خور وبا روش پیش بین وفقی

 

بنابراين الگوريتم ANC فيدبك دار به صورت يك پيش بين وفقي نويز اوليه d(n) عمل مي كند تا نويز خطاي باقيمانده e(n) را مينيمم كند.در نتيجه عملكرد الگوريتم و راندمان آن به قابل پيش بيني بودن نويز اوليه d(n)،بستگي پيدا مي كند.جزييات دقيق تحليل الگوريتم ANC فيدبك دار،به عنوان يك دستگاه پيش بين وفقي در [9] ارايه شده است.

مي دانيم كه سيگنال خطاي شكل 7-2 را مي توان به صورت زير بيان كرد:

 

                                  2-20 

                                               2-21       

                         2-22   

                              

وبا بازنويسي و مرتب سازي معادله 2-22و جاگذاري معادله 2-24 در رابطه 2-20 خواهيم داشت:

 

                    2-23  

                                        2-24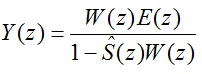

                                 2-25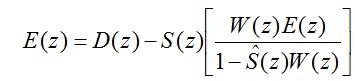                    

 

             2-26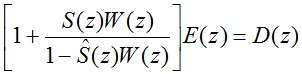  

 

                     2-27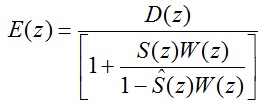   

 

 

              2-28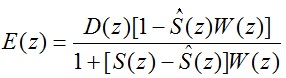                                                                                             

 

با فرض (s(z= رابطه 2-28 به صورت زير ساده مي شود.

 

           2-29

بنابراين تابع انتقال كلي سيستم ANC فيدبك دار از d(n) تا e(n) برابر است با:

                 2-30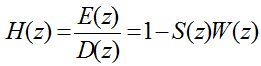 

در نتيجه در شرايط ايده آل،سيستم ANC فيدبك دار به يك سيستم ANC بدون فيدبك تبديل مي شود.

براي كاربرد هاي خاصي كه در آن نويز باند باريك است مي توان از روش سنتز شكل موج استفاده كرد.در اين روش از سيگنال مرجع توليد شده x(n) براي سنتز يك مولفه فركانس پايين،كه داراي نرخ سرعت تكراري قفل شده در بسامد اصلي محرك منبع نويز اوليه مي باشد،استفاده مي شود.تخمين سيگنال مرجع به صورت مستقم به حلقه قفل فاز داده مي شود كه يك پالس همزمان براي تركيب كننده² شكل موج،توليد مي كند.جزييات بيشتر در [20] ارايه شده است.

طرح هاي ديگري نيز براي ANC فيدبك دار ارايه شده اند.Oppenheim and Zangi [21] يك طرح ANC فيدبك دار مبتني بر الگوريتم block Expectation Maximize معرفي كرده اند و Openheim et al [22] روشي بر اساس الگوريتم RLS ارايه كرده است.البته اين الگوريتم ها با شرايط ايده آل ايجاد شده و شرايط اوليه آن ها بايد به دقت اجرا شود تا همگرايي الگوريتم تضمين شود.تحليل عملكردي و راندمان كليه اين الگوريتم ها نشان مي دهد كه تضعيف نويز در ناحيه فركانس هاي زير يك كيلو هرتز بسيار قابل توجه بوده و با افزايش فركانس مركزي نويز ، بدتر مي شود [3][19][24]. همچنین ناحیه تاثیر آنها برای تضعیفی در حدود 10dBدر فاصله کمتر از یک دهم طول موج نویز از بلندگوی مبدل سیگنال ضدنویزاست.به همین دلیل از این روشها غالبا در فضاهای بسته مثل اتاق ماشین یا کابین خلبان استفاده می شود.

 

---

1adaptive predictor

2synthesizer 

 

2-2 نظریه های مربوط به موضوع تحقیق

1-2-2 سيستم هاي ANC مركب (هيبريد)

تركيب تكنيك هاي ANC فيدبك دار و بدون فيدبك ، به عنوان تكنيك ANC مركب ( هيبريد ) شناخته مي شود.در اين حالت، سيگنال حذف شونده¹ بر اساس ورودي هاي هم سنسور مرجع و هم سنسور خطا ساخته مي شود.اين روش براي اولين بار توسط Swanson [27] ارايه شد.هدف اين روش،افزايش همبستگي بين نويز اوليه و سيگنال بدست آمده از سنسور مرجع مي باشد.از اين رو سنسور خطا معمولا در پايين دست منبع نويز اوليه، و سنسور مرجع تا حد ممكن در نزديكي منبع اوليه قرار داده مي شود.البته اغلب احتمال داد كه سنسور مرجع، كليه نشانه هاي آكوستيكي منبع نويز اوليه را بدست نياورد كه اين مساله با استفاده از سيگنال درون سنسور خطا براي توليد خروجي سیگنال حذف شونده، قابل حل مي باشد [19].بلوك دياگرام شماتيكي ANC مركب به صورت نشان داده شده در 9-2 است .

 

 

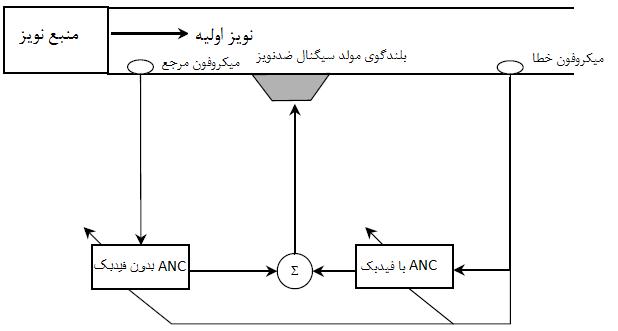
شکل(9-2) حذف فعال نویز با دو روش پس خور وبا پیش خور

 

سيستم شكل 9-2 با استفاده از مسير بدون فیدبك و به صورت هر كدام از موارد زير ، قابل پيكربندي است .

1 . الگوريتم Filtered-X LMS

2 . الگوريتم Filtered-X LMS با حذف فيدبك

3 . الگوريتم LMS بازگشتيFiltered-U²

مسير فيدبك به صورت يكي از حالات زير قابل پيكربندي است :

1 . ANC فيدبك دار كلاسيك

2 . ANC فيدبك دار با استفاده از الگوريتم Filtered-X LMS

3 . متد سفيد كردن³ خروجي

سيگنال حذف شونده داده شده به بلندگو معمولا يك مجموع غير وزن دار از خروجي هاي هر دو الگوريتم است.Vijayan [19] نشان داده كه طرح ANC مركب در حذف نويز پهن باند،در مقايسه با طرح هاي فيدبك دار يا بدون فيدبك به تنهايي،بهتر عمل مي كند.علاوه بر اين می توان طول فيلتر ها را در طرح مركب،كاهش داد.ANC پیش خور دار کاربرد های متعددی دارد.مثلا از آن در محفظه های شنوایی مانند گوشی ها [13][14][15][24]، به همراه سایر روش های پسیو برای کاهش نویز استفاده می شود. محصولات تجاری مختلفی نیز از روش ANC غیر وفقی برای حذف نویزاستفاده می کنند. بطور مثال سیستم حذف فعال نویز در کیت های یکپارچه گوشی های موبایل [25] و با استفاده از بلندگو و میکروفون درون خود موبایل،پیاده سازی می شود [26].در همه این موارد،آنتی نویز تولید شده باید با سیگنال مطلوب ( مانند سیگنال صوتی دریافتی یا سیگنال صوتی از یک منبع صدای خارجی ) ترکیب شود.بنابراین ممکن است سیگنال آنتی نویز ایجاد شده بوسیله سیستم ANC، باعث افت کیفیت سیگنال مطلوب نیز شود.

 

 

 

---

1Cancelling Signal

2Recursive LMS Algorithm

3Whitening

 

2-2-2 ANC‌ چند کاناله

در موارد زیادی مطلوب است که حذف نویز در چند نقطه از فضای سه بعدی انجام شود.سیستم های تک کانال در مواردی مفید و موثر می باشند که ناحیه مورد نظر،محدود باشد و فقط یک منبع اولیه با موقعیت دقیقا معین،و یک " ناحیه سکوت "¹ که سنسور خطا در آن واقع می شود،وجود داشته باشد.البته در بسیاری از کاربرد های عملی،فضای چند بعدی نسبتا بزرگی درگیر می شود و نمی توان منبع نویز را به طور دقیق در یک نقطه تنها تعیین کرد.پیچیدگی ANC چند کانال در فضای چند بعدی خیلی بیشتر است.

برترین مورد کاربرد سیستم های چند کاناله در کنترل نویز،صدای ناشی از اگزوز در اتاق اتومبیل و همچنین در کابین ماشین های سنگین ( مانند ماشین های خاک برداری ، هواپیما ها و . . . ) می باشد [29][30].معمولا این الگوریتم ها به صورت تک مرجع و با چند سنسور خطا می باشند.روش كار آن بر مبناي استفاده از يك سنسور آكوستيكي تنها،براي توليد سيگنال مرجع متناوب و مينيمم كردن مجموع مربعات خروجي هاي تعداد زيادي سنسور خطا كه در فاصله هاي مساوي از هم قرار دارند، است.معمولا در شرايطي كه محدوده پياده سازي ANC، بزرگ باشد الگوريتم هاي چند كاناله ضرورت پيدا مي كنند.Elliott[31] يك الگوريتم FXLMS چند كاناله را براي حذف نويز ماشينهای چرخشي معرفي كرده است كه با استفاده از سنسور هاي خطاي چند تايي و يك تك سنسور سيگنال مرجع غير آکوستيك،ايجاد مي شود.براي حالت هاي با چند مرجع و ANC بدون فيدبك پهن باند با چند خروجي،نيز ساختار هاي پردازش سيگنال معرفي شده اند [32].سيستم ANC چند كاناله معمولا نيازمند تحقيقات كامل و دقيق درباره خصوصيات آكوستيكي محيطي كه سيستم در آن پياده سازي مي شود،است.تابع انتقال مسير ثانويه معمولا داراي يك فاز غير مينیمم است يعني شامل صفر هايي در بيرون دايره واحد است ( به علت انعكاس هاي متعدد در فضاي سه بعدي).استراتژي كلي اين است كه انرژي نهايي را در فضاي چند بعدي (يعني مجموع خروجي هاي كليه سنسور ها)، مينيمم كنيم. در نتيجه محل قرار گيري اين سنسور ها از اهميت قابل توجهي برخوردار است به طوري كه مشخص كننده مجموع كلي انرژي در فضاي سه بعدي مي باشد.

بنابراين مي توان سيستم ANC بدون فيدبك چند كاناله را به عنوان تركيبي از سيستم هاي بدون فيدبك تك كانال در نظر گرفت،با اين تفاوت كه چند مسير ثانويه از هر فيلتر وفقي به هر سنسور خطا وجود دارد.معمولا  سيستم هاي بدون فيدبك چند كاناله نيز به علت تعداد زياد سنسور هاي خطا و مرجع،تمايل به فيدبك دار شدن دارند.همچنين در سيستم هاي چند كاناله، معمولا فيلتر هاي وفقي IIR نسبت به فيلتر هاي FIR موثر تر هستند [33].

 

---

 

1Quiet zone

3-2-2 ANCباندفرعی و ANCحوزه فركانس

سيستم هاي ANC بدون فيدبك در حوزه فركانس نيز قابل پياده سازي مي باشند. در اين حالت سيگنال مرجع x(n) ابتدا در يك بافر نقطه اي L ذخيره شده و سپس با استفاده از FFT نقطه L، به سيگنال حوزه فركانس تبديل مي شود. سپس طيف FFT در وزن هاي وفقي مناسب ضرب مي شود تا يك سيگنال خروجي حوزه فركانس بسازد كه پس از آن با استفاده از IFFT نقطه L به حوزه زمان تبديل خواهد شد.

 

 

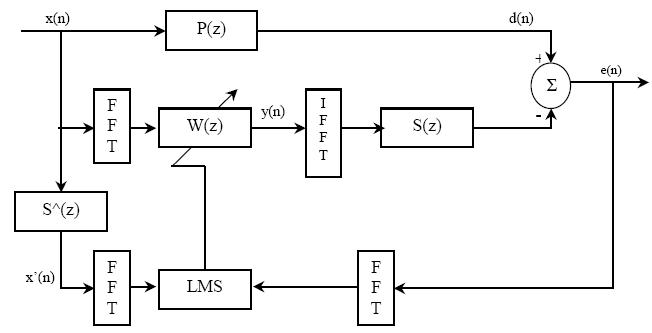
شکل (10-2)  ساختار FXLMS پیش خور دار در حوزه فرکانس

 

سيستم نشان داده شده در شكل 10-2 براي اولين بار توسط Shem and Spanias[34] ارايه شد و پس از آن به صورت چند كاناله تعميم يافت [35]. Reichard and Swanson [36] يك ساختار  FXLMS بدون فيدبك حوزه فركانس را با استفاده از مشخصه سيستم آنلاين، پياده سازي كردند. Feintuch et al [37] نشان داده كه تا زماني كه باند فركانسي مورد نظر، محدود باشد، قبل از فرآيند تطبيق، واقعا نيازي به تخمين تابع انتقال مسير ثانويه وجود ندارد و فقط بايد تاخير ناشي از تايع انتقال در باند فركانسي را بدانيم.اشكال اصلي الگوريتم حوزه فركانس اين است كه داده ها را به صورت بلوك به بلوك به جاي نمونه به نمونه¹ پردازش مي كند. بنابراين L نمونه تاخير بين ورودي سيگنال مرجع و خروجي سيگنال آنتي نويز ثانويه وجود دارد.اين تاخير براي نويز پريوديك فركانس پايين،تقريبا قابل تحمل است ولي در نويز حالت پهن باند،وقتي الگوريتم FXLMS حوزه فركانس با سیستم ANC پیش خور دار،انطباق يافته است اين تاخير برابر 2L می شود چون L نمونه تاخیری دیگر نیز در هنگام بازتولید سیگنال مرجع،بوجود می آید.بنابراین پیاده سازی ساختار FXLMS پیش خور دار در حوزه فرکانس، بسیار نامناسب است.

 

---

1Sample by sample

4-2-2 ANCباندفرعی¹

ANC دارای کاربرد های متعددی در حذف نویز پهن باند می باشد.برای این که بتوان به صورت کارآمد و موثری  نویز پهن باند را حذف نمود لازم است که از فیلتر های وفقی با صدها تپ (Tap) استفاده شود. این فیلتر ها دارای نرخ همگرایی کندی هستند.به علاوه از ANC به صورت ترکیب در کاربردهای دیگر نیز استفاده می شود.در این حالت از بلندگو هم برای پخش سیگنال آنتی نویز و هم پخش سیگنال مطلوب از یک منبع ثانویه استفاده می شود و سنسور خطا هم سیگنال مطلوب و هم نویز باقیمانده را دریافت می کند.در نتیجه احتمال دارد که سیگنال آنتی نویز ایجاد شده باعث افت کیفیت سیگنال مطلوب نیز شود.تکنیک های فیلترینگ وفقی باند فرعی برای حل این گونه مشکلات در حذف بازتاب آکوستیکی و ارتقای کیفیت سیگنال، به کار می روند [38].Morgan and Thi [39] ساختاری برای ANC پس خور ارایه داده اند که بسیار مشابه ساختار حوزه فرکانسی است که قبلا معرفی شده است.یعنی وزن های وفقی برای هر باند فرعی² به صورت مجزا محاسبه می شود و سپس به یک فیلتر پهن باند معادل آن ارسال می شود.تفاوت این روش با ساختار حوزه فرکانس در این است که پردازش واقعی سیگنال باند فرعی،در حوزه زمان رخ می دهد.این تکنیک از نظر محاسباتی،قدرتمند است چون باید FFT چند فاز روی سیگنال مرجع فیلتر شده و سیگنال خطا،و همچنین FFT معکوس روی وزن های فیلتر انجام شود.البته هنوز نسبت به فیلتر وفقی پهن باند معادل،دارای قدرت کمتری است [40].Park et al [41] با اعمال تغییرات و اصلاحاتی روی معماری فیلتر وفقی باند فرعی، تابع انتقال مسیر ثانویه را هم به یک سری ازباندهای فرعی تجزیه می کند.در هر دو این مطالعات مشاهده می شود که تکنیک باند فرعی در مقایسه با الگوریتم FXLMS پهن باند مرسوم،به طور قابل ملاحظه ای همگرایی بهتری دارد و اهمیت این تکنیک در صورت استفاده از ANC همراه با کاربرد های دیگر،بیشتر خواهد بود.Hussain and Campbell [42] درباره کاربرد های ANC باند فرعی برای صدای گفتاری که با نویز اتومبیل،خراب شده است مطالعاتی انجام دادند.آن ها در روش خود از دو کانال مجزا استفاده کردند که تکنیک باند فرعی برای هر کانال به صورت جداگانه اعمال می شود.البته این تکنیک ها در سیستم FXLMS پیش خور دار،به علت نیاز به بافر کردن سیگنال مرجع و سیگنال خطا به خوبی جواب نمی دهد.

روش ها و تکنیک هایی برای فیلترینگ باند فرعی با استفاده از بانک فیلتری³ معرفی شده اند.مثلا Vitterli and Gilloire [43] and Usevitch and Orchard [44] هر کدام به صورت جداگانه روشی برای فیلترینگ باند فرعی ارایه داده اند که در آن سیگنال مورد انتظار و سیگنال خطا،با استفاده از یک بانک فیلتری به باند های فرعی تقسیم می شوند و هر باند فرعی به صورت مستقل،پردازش میشود. Petraglia and Alves [45] درباره شرایط این بانک فیلتری،و Alves et al [46] در زمینه خصوصیات همگرایی ساختار فیلتر وفقی باند فرعی تحقیق کرده اند.استفاده از روش بانک فیلتری برای ANC پیش خور دار باند فرعی،مناسب تر است چون پردازش می تواند روی هر نمونه پایه انجام شود.

 

---

1Subband

2FFT bin

3Filterbanks 

فصل سوم : روش تحقیق 

1-3 شروع به کار با فیلتر های وفقی (ADAP-FILT Objects )

در این قسمت نحوه استفاده از الگوریتم فیلتر وفقی موجود در جعبه ابزار طراحی فیلتر¹MATLAB نشان داده می شود. با وجود اینکه حدود 30 الگوریتم مختلف فیلترینگ وفقی مرتبط با جعبه ابزار طراحی فیلتر MATLAB وجود دارد، ما تنها دو الگوریتم از آن ها را به کار می بریم. برای مشاهده لیست کلیه الگوریتم ها و متد های کاربردی فیلترهای وفقی ازدو عبارت " helpwin adaptfilt " و یا " help adaptfilt " استفاده می شود وبرای مشاهده متون کمکی درباره یک الگوریتم خاص مثلا الگوریتم lms "helpadaptfilt/lms " را تایپ و اجرا می کنیم. اکنون به بیان مثالی ساده می پردازیم.

 

---

1Filter Design Toolbox

 

1-1-3 سیگنال مطلوب

می خواهیم از یک فیلتر وفقی برای جدا کردن سیگنال مطلوب از یک سیگنال آلوده به نویز ( بوسیله روش حذف فعال نویز ) استفاده کنیم. سیگنال مطلوب به صورت سینوسی می باشد.

 

n = (1:1000)';

s = sin(0.075*pi*n);

2-1-3 سیگنال نویز

فرض می کنیم که سیگنال نویز v1 به صورت autoregressive ( استفاده از آمار های قبلی به عنوان پایه ای برای پیش بینی داده های آینده ) باشد .

v = 0.8*randn(1000,1);

ar = [1,1/2];

v1 = filter(1,ar,v);

3-1-3 سیگنال آلوده به نویز

سیگنال سینوسی آلوده به نویز به سادگی با جمع s+v1 بدست می آید.

x = s + v1;

4-1-3 سیگنال مرجع

فرض می کنیم که یک سیگنال میانگین متحرک v2 که با v1 همبسته است در اختیار داریم . از این سیگنال به عنوان سیگنال مرجع استفاده می کنیم.

ma = [1, -0.8, 0.4 , -0.2];

v2 = filter(ma,1,v);

5-1-3 ساخت فیلتر های وفقی

ما از دو فیلتر وفقی که هر یک دارای 7Tap ( وزن ) هستند، یک فیلتر LMS، و یک فیلتر LMS نرمالیزه ( NLMS) استفاده می کنیم.

L = 7;

hlms = adaptfilt.lms(7);

hnlms = adaptfilt.nlms(7);

6-1-3 انتخاب اندازه گام ( step size )

کلیه الگوریتم های مشابه LMS دارای یک مقدار غیر دقیق برای اندازه گام هستند که تعیین کننده میزان تصحیح خطای فیلتر در هر مرحله تکرار تطبیق شدن فیلتر می باشد. انتخاب مقدار مناسب و صحیح برای این اندازه گام همواره ساده نیست . اگر اندازه گام کوچک باشد ، سرعت همگرایی فیلتر افت می کند و اگر بزرگ باشد ممکن است منجر به واگرا شدن فیلتر شود. در جعبه ابزار طراحی فیلتر، الگوریتم هایی برای تعیین حداکثر مقدار مجاز اندازه گام برای تضمین همگرایی در این گونه الگوریتم ها وجود دارد. برای کسب اطلاعات بیشتر، ازدستور helpwin adaptfilt/maxstep استفاده می کنیم.

 

[mumaxlms,mumaxmselms]   = maxstep(hlms,x)

[mumaxnlms,mumaxmsenlms] = maxstep(hnlms);

 

mumaxlms =

0.21548

mumaxmselms =

0.12642

7-1-3 تنظیم اندازه گام

اولین خروجی Maxstep برابر مقدار مورد نیازبرای همگرایی ضرایب ودومین خروجی آن برابر مقدار مورد نیاز برای همگرایی میانگین مربعات ضرایب می باشد.البته انتخاب مقادیر بزرگ برای اندازه گام نیز می تواند منجر به نوسانات زیاد در مقادیر همگرایی شود و بنابراین ما مقادیر کوچکی را برای اندازه گام برمی گزینیم.

hlms.StepSize  = mumaxmselms/30;

hnlms.StepSize = mumaxmsenlms/20;

با مشخص کردن اندازه گام مورد استفاده،می توانیم مقادیر آن را در هنگام ساخت اولین فیلتر نیز تنظیم کنیم:

hlms = adaptfilt.lms(N,step);

8-1-3 فیلترینگ با فیلتر های وفقی

با داشتن پارامتر های فیلتر های وفقی می توان سیگنال آلوده به نویز را فیلتر نمود.در این مرحله فرض می کنیم v2 سیگنال مرجع ورودی فیلتر وفقی، و  x سیگنال مطلوب است.هدف این است که خروجی فیلتر (y) بیشترین شباهت ممکن را با x داشته باشد.البته ازآنجا که ورودی فیلتر وفقی (v2)، تنها به مولفه نویز x یعنی (v1) وابسته است فقط می تواند همان را شبیه سازی کند.سیگنال خطا (در اینجا برابر سیگنال مطلوب x منهای خروجی واقعی y)،تخمینی از بخشی از سیگنال را که با v2 همبسته نیست را ایجاد کند که همان سیگنالی است که می خواهیم آن را از x استخراج کنیم و به نام s می باشد.

[ylms,elms] = filter(hlms,v2,x);

[ynlms,enlms] = filter(hnlms,v2,x);

9-1-3 روش حل بهینه

برای مقایسه،فیلتر بهینه FIR Wiener را محاسبه خواهیم کرد.

bw = firwiener(L-1,v2,x);

yw = filter(bw,1,v2);  

ew = x - yw;

10-1-3 نمودارهای نتایج

 

 

اکنون یک تقریب سینوسی برای هر مورد را نشان خواهیم داد.

 

 

plot(n(900:end),[ew(900:end), elms(900:end),enlms(900:end)]);

legend('Wiener filter denoised sinusoid',...

    'LMS denoised sinusoid', 'NLMS denoised sinusoid');

xlabel('Time index (n)');

ylabel('Amplitude');

 

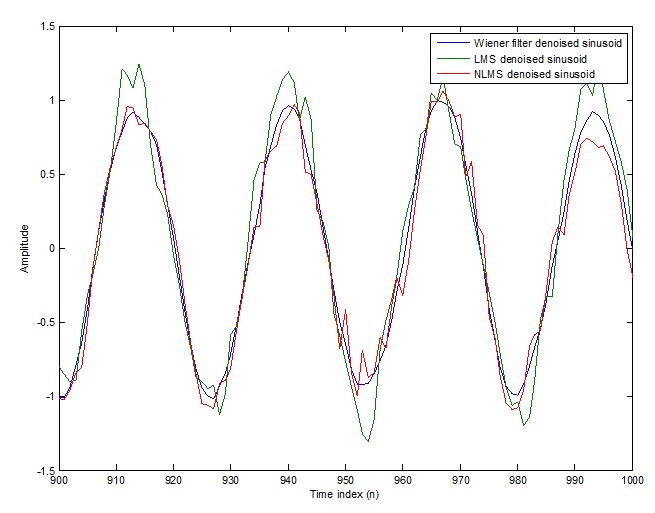
شکل (1-3)  نمودار FIR Wiener وLMS وNLMS

 

سیگنال آلوده به نویز را به صورت نقطه نقطه نشان می دهیم تا به عنوان مرجع استفاده شود.

 

hold on

plot(n(900:end),x(900:end),'k:')

xlabel('Time index (n)');

ylabel('Amplitude');

hold off

 

 

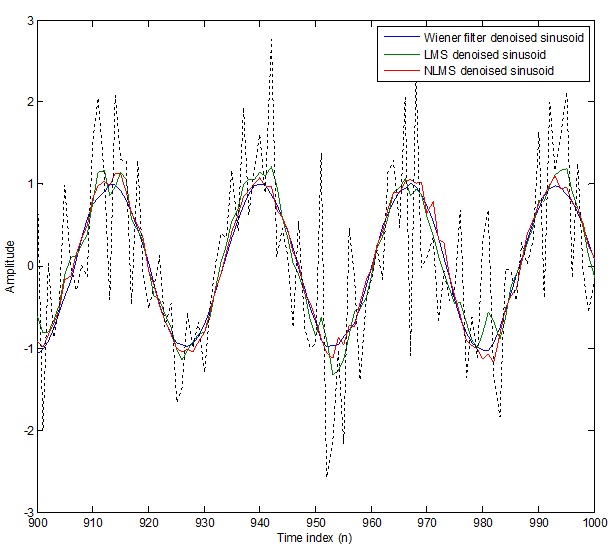
شکل (2-3) نمودار FIR Wiener وLMS وNLMS

 

11-1-3 ضرایب نهایی

می توانیم ضرایب فیلتر FIR Wiener را با فیلتر های وفقی مقایسه کنیم.فیلتر های بایدبه ضرایب Wiener همگرا شوند .

 

[bw.' hlms.Coefficients.' hnlms.Coefficients.']

ans =

    1.0016    0.8869    1.0419

    0.3058    0.1381    0.3766

    0.1006   -0.0063    0.1657

    0.0406   -0.0069    0.0888

    0.1248    0.0804    0.1863

    0.0799    0.0319    0.1097

    0.0349    0.0240    0.0634

 

12-1-3 تنظیم مجدد فیلتر قبل از فیلترینگ

فیلتر های وفقی دارای یک شاخص " PersistentMemory " می باشند که برای آزمایشات دقیق مورد استفاده قرار می گیرد. به صورت پیش فرض، این شاخص "false" است که به معنای تنظیم مجدد وضعیت و ضرایب فیلتر، قبل از فیلترینگ می باشد. مثلا دو فراخوانی  بعدی، در هر دو حالت خروجی یکسانی تولید می کنند.

 

[ylms,elms] = filter(hlms,v2,x);

[ylms2,elms2] = filter(hlms,v2,x);

 

برای حفظ مقادیر قبلی فیلتر در هنگام فیلترینگ مقادیر داده جدید، باید این شاخص را off کنیم. در این صورت، وضعیت و ضرایب نهایی یک اجرای قبل، به عنوان شرایط اولیه برای مجموعه بعدی داده ها مورد استفاده قرار می گیرد.

 

[ylms,elms] = filter(hlms,v2,x);

hlms.PersistentMemory = true;

[ylms2,elms2] = filter(hlms,v2,x);

 

اگر شاخص را True کنیم برای فیلترینگ مقادیر بزرگ داده ( که می تواند به قسمت های کوچک تر بخش بندی شود و سپس به استفاده از یک حلقه For به ورودی فیلتر داده شود) مفید است .

13-1-3 منحنی های یادگیری

 

برای آنالیز همگرایی فیلتر های وفقی ، منحنی های یادگیری را بررسی می کنیم . این کار را می توان به سادگی با استفاده از جعبه ابزار طراحی فیلتر MATLAB انجام داد ولی برای بدست آوردن نتایج دقیق و مشخص باید آزمایشات بیشتری انجام دهیم. ما از 25 نمونه سینوسی نویزی استفاده می کنیم.

 

n = (1:5000)';

s = sin(0.075*pi*n);

nr = 25;

v = 0.8*randn(5000,nr);

v1 = filter(1,ar,v);

x = repmat(s,1,nr) + v1;

v2 = filter(ma,1,v);

14-1-3 محاسبه منحنی های یاد گیری

اکنون به محاسبه خطای میانگین مربعات می پردازیم. برای افزایش سرعت، خطا را یک بار برای هر ده نمونه محاسبه می کنیم. ابتدا باید فیلتر های وفقی را دوباره تنظیم کنیم تا از استفاده مجدد از ضرایبی که قبلا محاسبه شده اند و وضعیت های ذخیره شده، جلوگیری شود.

 

reset(hlms);

reset(hnlms);

M = 10;

mselms = msesim(hlms,v2,x,M);

msenlms = msesim(hnlms,v2,x,M);

plot(1:M:n(end),[mselms,msenlms])

legend('LMS learning curve','NLMS learning curve')

xlabel('Time index (n)');

ylabel('MSE');

 

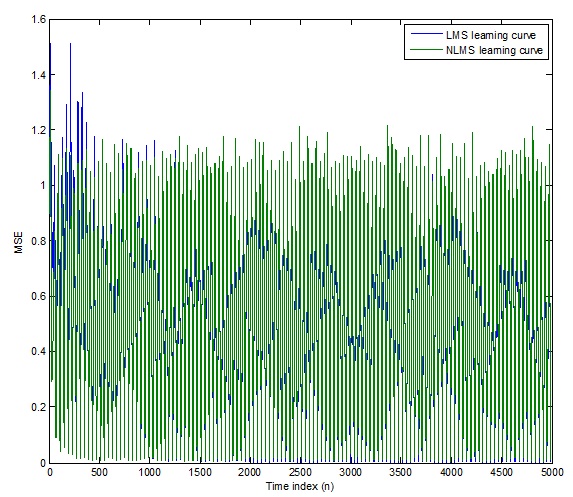
شکل (3-3) - نمودار منحنی های یادگیریLMS و  NLMS

 

15-1-3 منحنی های یادگیری تئوری

 

برای الگوریتم های LMS و NMLS، منحنی های یادگیری نیز همراه با مینیمم خطای میانگین مربعات (MMSE)، خطای میانگین مربعات اضافی (EMSE)،  و مقدار متوسط ضرایب قابل محاسبه هستند .

 

reset(hlms);

[mmselms,emselms,meanwlms,pmselms] = msepred(hlms,v2,x,M);

plot(1:M:n(end),[mmselms*ones(500,1),emselms*ones(500,1),...

        pmselms,mselms])

legend('MMSE','EMSE','predicted LMS learning curve',...

    'LMS learning curve')

xlabel('Time index (n)');

ylabel('MSE');

 

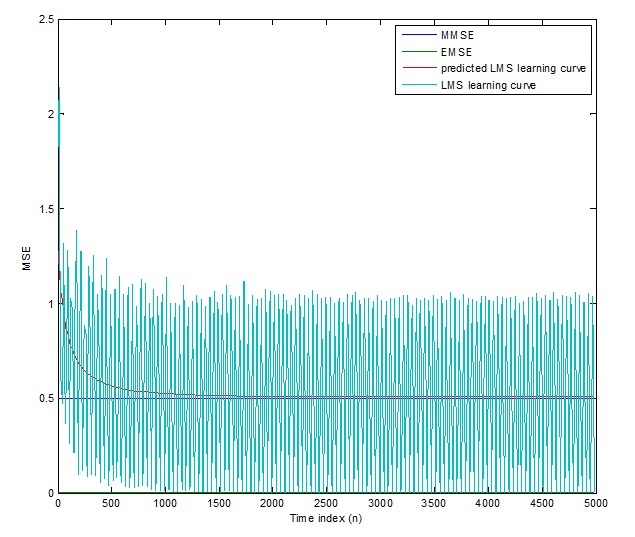
شکل (4-3) نمودار منحنی های یادگیریLMS وNLMS و مینیمم خطای میانگین مربعات (MMSE) و خطای میانگین مربعات اضافی ( EMSE )

 

2-3 حذف نویز وفقی با استفاده از فیلترینگ وفقی RLS

در این مثال می خواهیم توانایی فیلتر RLS را در استخراج اطلاعات مفید از یک سیگنال آلوده به نویز نشان دهیم. این سیگنال اطلاعات به صورت یک موج سینوسی می باشد که نویز سفید گوسی به آن افزوده شده است.

فرض می کنیم که سیستم حذف نویز از دو میکروفون استفاده می کند. یک میکروفون اولیه که سیگنال نویز را می گیرد و یک میکروفون  ثانویه که نویزی را دریافت می کند که با سیگنال حاوی اطلاعات، ناهمبسته و با نویز دریافتی بوسیله میکروفون اولیه، همبستگی دارد.

سیگنال حاوی اطلاعات به صورت یک موج سینوسی با 0.055 cycles/sample می باشد.

 

signal = sin(2*pi*0.055*(0:1000-1)');

plot(0:199,signal(1:200));

grid; axis([0 200 -2 2]);

title('The information bearing signal');

 

 

                                                               

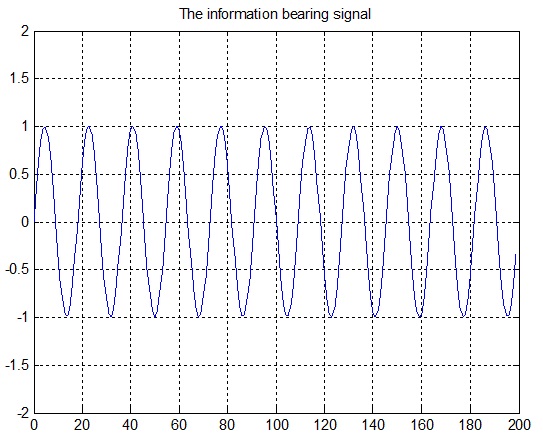
شکل (5-3) سیگنال اولیه بدون نویزحاوی اطلاعات

 

نویز دریافتی توسط میکروفون ثانویه، ورودی فیلتر وفقی RLS می باشد. نویز آلوده کننده موج سینوسی، حالت فیلتر پایین گذر (همبسته) این نویز است. سیگنال مطلوب برای فیلتر وفقی، معادل حاصل جمع نویز فیلتر شده و سیگنال حامل اطلاعات می باشد.

 

nvar  = 1.0;                 

noise = randn(1000,1)*nvar;  

plot(0:999,noise);

title('Noise picked up by the secondary microphone');

grid; axis([0 1000 -4 4]);

 

 

 

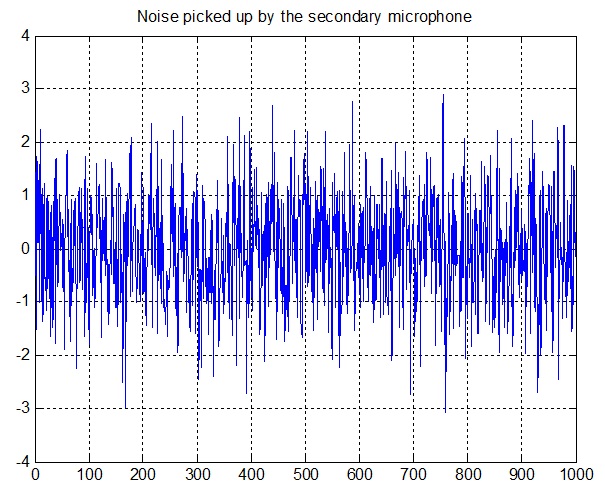
شکل(6-3) نمودار نویز دریافتی توسط میکروفون ثانویه

 

نویز تخریب کننده سیگنال حامل اطلاعات، شکل فیلتر شده این "نویز" است.

 

nfilt  = fir1(31,0.5);            

fnoise = filter(nfilt,1,noise);   

 

سیگنال مطلوب برای فیلتر وفقی(موج سینوسی + نویز فیلتر شده):

 

d  = signal+fnoise;

plot(0:199,d(1:200));

grid; axis([0 200 -4 4]);

title('Desired input to the Adaptive Filter = Signal + Filtered Noise');

 

 

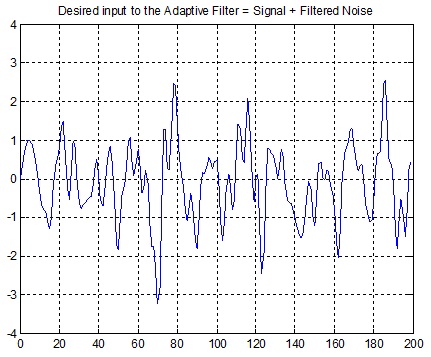
شکل(7-3) سیگنال ورودی فیلتر وفقی ( موج سینوسی + نویز فیلتر شده )

 

 

تنظیمات و مقدار دهی اولیه برای مقادیر و پارامتر های فیلتر وفقی RLS :

 

M = 32;                   

lam = 1;                  

delta = 0.1;              

w0 = zeros(M,1);          

P0 = (1/delta)*eye(M,M);  

Zi = zeros(M-1,1);        

 

پس از همگرایی فیلتر وفقی ، نویز فیلتر شده باید به طور کامل از سیگنال "سیگنال+نویز" کاسته شود و سیگنال خطا "e" باید فقط شامل سیگنال اصلی اولیه باشد .

 

plot(0:499,signal(1:500),0:499,e(1:500)); grid;

axis([0 500 -4 4]);

title('Original information bearing signal and the error signal');

legend('Original Signal','Error Signal');

 

 

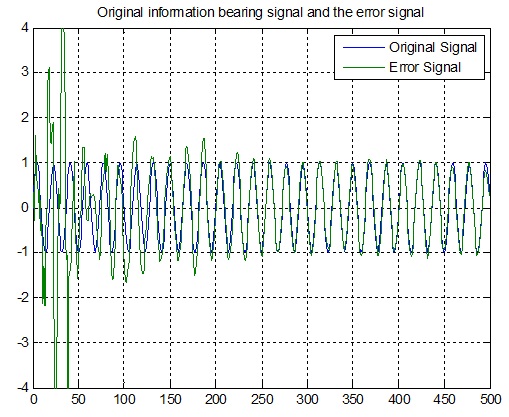
شکل(8-3) نمودار سیگنال اصلی حاوی اطلاعات در برابر سیگنال خطا

3-3 پیش بینی خطی با استفاده از فیلتر وفقی NLMS

در این مثال به طرح فیلتر وفقی NLMS‌( حداقل میانگین مربعات نرمالیزه ) در یک ساختارپیش بینی خطی می پردازیم. نمونه حاضر از موج سینوسی آلوده به نویز، با استفاده از 32 نمونه قبلی، پیش بینی شده است یعنی فیلتر وفقی NLMS مرتبه 32 ام بر روی داده ها اعمال شده است . سیگنال مطلوب به صورت یک موج سینوسی با 0.015 cycles/sample و یک کسینوس با 0.008 cycles/sample می باشد .

N = 500;

N = 500;

sig = [sin(2*pi*0.015*(0:N-1)) 0.5*cos(2*pi*0.008*(0:N-1))];

plot(0:2*N-1,sig); grid;

title('Desired Input to the Adaptive Filter');

 

 

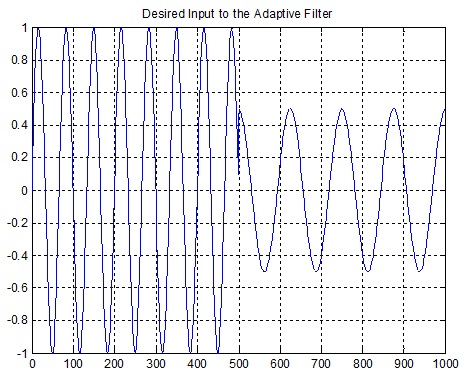
شکل(9-3) سیگنال مطلوب ورودی به فیلتر وفقی

 

ورودی فیلتر وفقی به صورت شکل تاخیر یافته سیگنال مطلوب می باشد که بوسیله نویز با واریانس 0.5 خراب شده است.

 

nvar = 0.5;                  

noise  = nvar*randn(1,2*N);  

n = sig + noise;             

x = [0 n];                   

d = [sig 0];                  

M = 32;                      

mu = 0.2;                    

plot(0:2*N,x); grid;

title('Input to the Adaptive Filter');

 

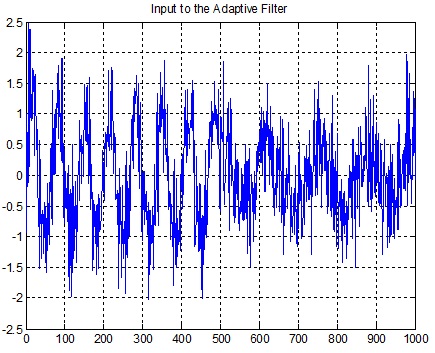
شکل(10-3) سیگنال ورودی به فیلتر وفقی

 

ساخت و به کار گیری فیلتر وفقی LMS نرمالیزه با طول 32 ، اندازه گام (Step Size)، برابر 0.2 و آفست برابر 1e-6.

 

 

Hadapt = adaptfilt.nlms(M,mu,1,1e-6);

[y,e] = filter(Hadapt,x,d);

cla;

plot(0:1000,[d' y']);

grid on;

axis([0 1000 -2 2]);

title('Adaptive Linear Prediction');

legend('Actual Signal','Predicted Signal');

 

 

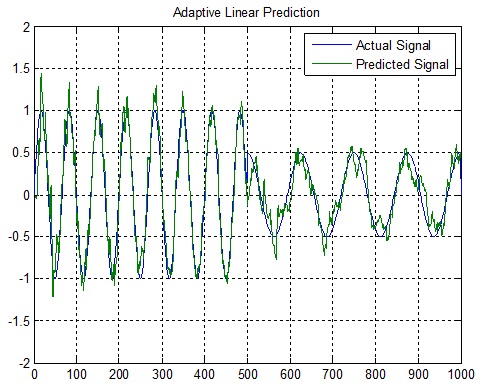
شکل(11-3) نمودار سیگنال واقعی دربرابر سیگنال پیش بینی شده

FX-LMS  4-3شبیه سازی روش حذف فعال نویز با استفاده از الگوریتم

1-4-3 مسیر انتشار ثانویه

مسیر انتشار ثانویه مسیری است که سیگنال آنتی نویز از بلندگوی خروجی تا میکروفون خطا در ناحیه ساکت می پیماید. دستورات زیر، یک پاسخ ضربه از بلندگو تا میکروفون خطا تولید می کنند که پهنای باند آن در محدوده 50-1000 هرتز قرار دارد و با طول فیلتر 0.1 ثانیه می باشد.

 

Fs = 8000;

N = 800;

delayS = 7;

Fd = fdesign.bandpass('N,Fst1,Fst2,Ast',8,0.0125,0.25,20);

Hd = design(Fd,'cheby2','FilterStructure','df2tsos');

H = filter(Hd,[zeros(1,delayS) log(0.99*rand(1,N-delayS)+0.01).* ...

    sign(randn(1,N-delayS)).*exp(-0.01*(1:N-delayS))]);

H = H/norm(H);

t = 1/Fs:1/Fs:N/Fs;

plot(t,H,'b');

xlabel('Time [sec]');

ylabel('Coefficient value');

title('True Secondary Path Impulse Response');

 

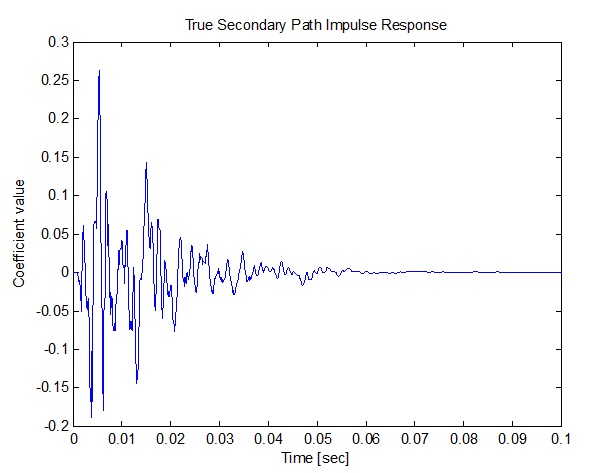
شکل(12-3)  پاسخ ضربه مسیرثانویه

 

2-4-3 تخمین مسیر انتشار ثانویه

اولین مساله در سیستم ANC، تخمین پاسخ ضربه مسیر انتشار ثانویه می باشد. این مرحله معمولا قبل از مرحله کنترل نویز با استفاده از سیگنال تصادفی پخش شده از بلند گوی خروجی ( در غیاب نویز نامطلوب)، اجرا می شود. دستورات زیر، 3.75 ثانیه از این نویز تصادفی و همچنین سیگنال اندازه گیری شده در میکروفون خطا را تولید می کنند.

 

ntrS = 30000;

s = randn(1,ntrS);

dS = filter(H,1,s) + 0.01*randn(1,ntrS);

3-4-3 طراحی روش تخمین مسیر انتشار ثانویه

معمولا طول تقریب فیلتر مسیر ثانویه، به اندازه مسیر ثانویه واقعی نمی باشد و در اکثر موارد برای کنترل مناسب نیست. ما باید از یک فیلتر مسیر ثانویه با طول 250 Tap (متناسب با طول پاسخ ضربه 31 میلی ثانیه) استفاده کنیم. برای این منظور می توان از هر الگوریتم فیلترینگ FIR وفقی استفاده کرد ولی غالبا از الگوریتم LMS نرمالیزه ، به علت سادگی و قدرتمندی آن، استفاده می کنیم. نمودار های سیگنال های خطا و خروجی نشان می دهند که همگرایی این الگوریتم پس از حدود 10000مرتبه تکرار رخ می دهد.

 

 

M = 250;

muS = 0.1; offsetS = 0.1;

h = adaptfilt.nlms(M,muS,1,offsetS);

[yS,eS] = filter(h,s,dS);

n = 1:ntrS;

plot(n,dS,n,yS,n,eS);

xlabel('Number of iterations');

ylabel('Signal value');

title('Secondary Identification Using the NLMS Adaptive Filter');

legend('Desired Signal','Output Signal','Error Signal');

 

 

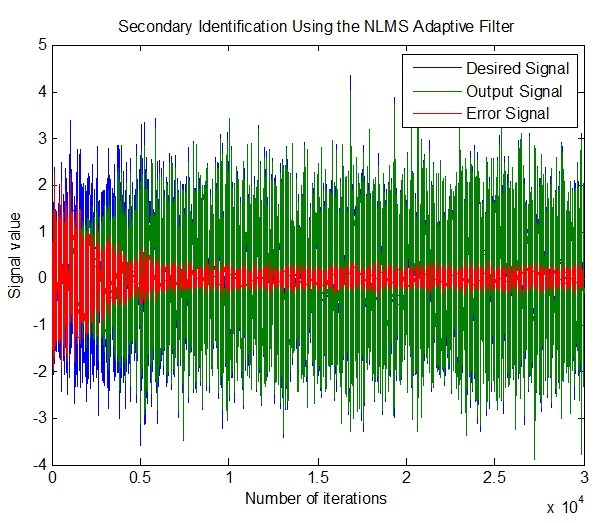
شکل(13-3) نمودار های سیگنال های مطلوب(واقعی)- خروجی و سیگنال خطای ناشی از تفاوت این دو سیگنال

4-4-3 دقت تخمین مسیر ثانویه

میزان دقت تخمین پاسخ ضربه مسیر ثانویه چقدر است ؟ این نمودار نشان دهنده ضرایب هر دو مسیر تخمین زده شده و مسیر واقعی است. فقط انتهای پاسخ ضربه واقعی، به خوبی تقریب زده نمی شود. این خطای باقیمانده نمی تواند چندان روی راندمان عملکرد سیستم ANC تاثیر نامطلوب داشته باشد.

 

Hhat = h.Coefficients;

plot(t,H,t(1:M),Hhat,t,[H(1:M)-Hhat(1:M) H(M+1:N)]);

xlabel('Time [sec]');

ylabel('Coefficient value');

title('Secondary Path Impulse Response Estimation');

legend('True','Estimated','Error');

 

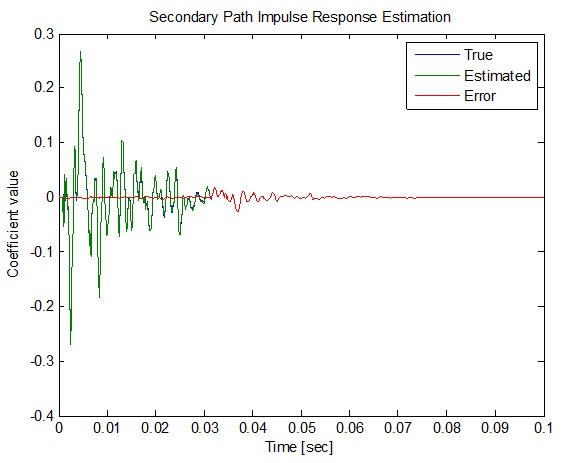
شکل(14-3) نمودار دقت تخمین مسیر ثانویه

5-4-3 مسیر انتشار اولیه

مسیر انتشار نویزی که می خواهیم آن را حذف کنیم نیز توسط یک فیلتر خطی قابل توصیف است. در ادامه دستورات تولید کننده پاسخ ضربه یک میکروفون ورودی-به-خطا ( با محدوده باند بین50 تا 1000 هرتز و فیلتر با طول 0.1 ثانیه ) ارایه خواهد شد.

 

delayW = 15;

Fd2 = fdesign.bandpass('N,Fst1,Fst2,Ast',10,0.0125,0.25,20);

Hd2 = design(Fd2,'cheby2','FilterStructure','df2tsos');

G = filter(Hd2,[zeros(1,delayW) log(0.99*rand(1,N-delayW)+0.01).*...

    sign(randn(1,N-delayW)).*exp(-0.01*(1:N-delayW))]);

G = G/norm(G);

plot(t,G,'b');

xlabel('Time [sec]');

ylabel('Coefficient value');

title('Primary Path Impulse Response');

 

 

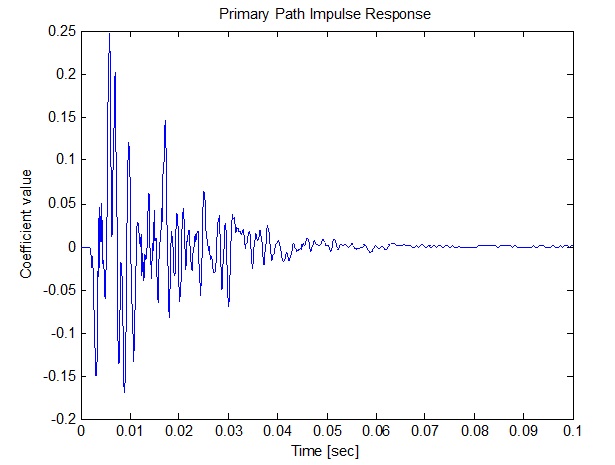
شکل(15-3) پاسخ ضربه واقعی مسیر انتشار اولیه

 

6-4-3 نویز مورد نظر برای حذف

متداول ترین کاربرد های ANC به حذف صدای ماشین های چرخشی، به علت آزار دهنده بودن این صدا، مربوط می شود. ما 7.5 ثانیه از یک نویز را به صورت مصنوعی تولید کرده ایم که از یک موتور الکتریکی معمولی ناشی می شود. این صدا در میکروفون خطا و قبل از اجرای حذف نویز، خصوصیات صدای یک موتور صنعتی معمولی را شبیه سازی می کند. طیف این صدا نیز در نمودار نشان داده است.

 

ntrW = 60000;

F0 = 60;

n = 1:ntrW;

A = [0.01 0.01 0.02 0.2 0.3 0.4 0.3 0.2 0.1 0.07 0.02 0.01];

x = zeros(1,ntrW);

for k=1:length(A);

    x = x + A(k)*sin(2*pi*(F0*k/Fs*n+rand(1)));

end

d = filter(G,1,x) + 0.1*randn(1,ntrW);

Hp = spectrum.welch; Hp.SegmentLength = 4444;

FFTLength=256;

Pd = psd(Hp,d(ntrW-20000:ntrW),'NFFT',8192,'Fs',Fs);

plot(Pd)

axis([0 2 -70 0]);

title('Power Spectral Density of the Noise to be Cancelled');

p8K = audioplayer(d/max(abs(d)),Fs);

playblocking(p8K);

 

 

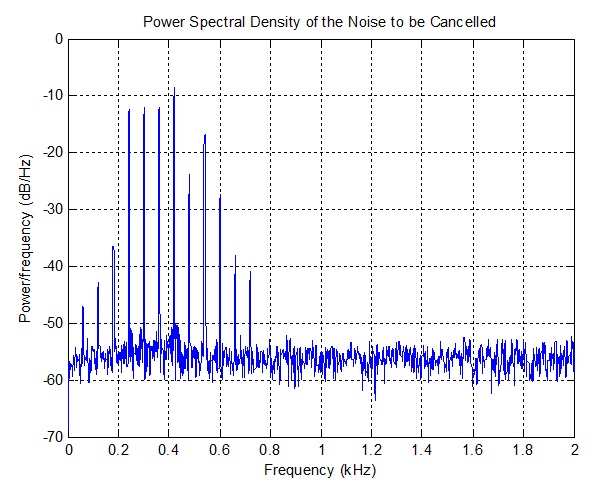
شکل(16-3) طیف نویز شبیه سازی شده صدای موتورالکتریکی است.

 

7-4-3 ANC با استفاده از الگوریتم FX-LMS

محبوب ترین الگوریتم وفقی برای ANC، الگوریتم FX-LMS می باشد. این الگوریتم از تخمین مسیر ثانویه برای محاسبه یک سیگنال خروجی استفاده می کند که در محل سنسور خطا، با نویز نامطلوب مقابله و آن را تضعیف می کند. سیگنال مرجع، یک شکل نویز دار از صدای نامطلوب اندازه گیری شده در نزدیکی منبع آن می باشد. ما باید از یک فیلتر کنترل کننده با طول حدودا 44 میلی ثانیه و اندازه گام ( step ) برابر 0.0001 برای این سیگنال ها، استفاده کنیم. همگرایی الگوریتم حاصل حدودا پس از 5 ثانیه از تطبیق پذیری رخ می دهد و صدای آزار دهنده موتور الکتریکی به طور قابل ملاحظه ای کاهش می یابد.

 

xhat = x + 0.1*randn(1,ntrW);

L = 350;

muW = 0.0001;

h = adaptfilt.filtxlms(L,muW,1,Hhat);

[y,e] = filter(h,xhat,d);

plot(n,d,'b',n,y,'g',n,e,'r');

xlabel('Number of iterations');

ylabel('Signal value');

tstr = ['Active Noise Control Using', ...

    ' the Filtered-X LMS Adaptive Controller'];

title(tstr);

legend('Original Noise','Anti-Noise','Residual Noise');

p8K = audioplayer(e/max(abs(e)),Fs);

playblocking(p8K);

 

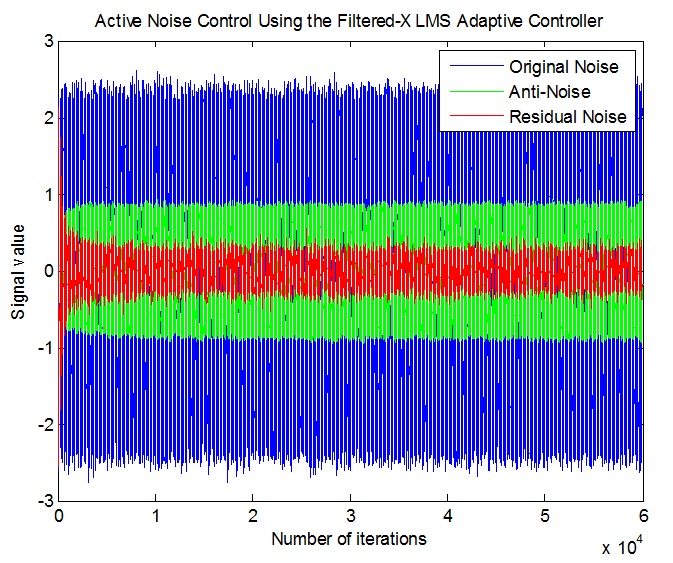
شکل(17-3) ANC با استفاده از الگوریتم FX-LMS

 

8-4-3 طیف سیگنال خطای باقیمانده

با مقایسه طیف سیگنال خطای باقیمانده با سیگنال نویز اولیه مشاهده می شود که اغلب مولفه های متناوب و پریودیک به طور چشمگیری تضعیف شده اند. راندمان حذف نویز در حالت پایدار برای کلیه فرکانس های، یکنواخت نمی باشد (مانند سیستم های دنیای واقعی).

 

Pe = psd(Hp,e(ntrW-20000:ntrW),'NFFT',8192,'Fs',Fs);

plot(Pd.Frequencies,10*log10(Pd.Data(:,1)),'b',...

    Pe.Frequencies,10*log10(Pe.Data(:,1)),'r');

axis([0 2000 -70 0]);

grid on

xlabel('Frequency (Hz)');

ylabel('Power/frequency (dB/Hz)');

tstr = ['Power Spectral Density of the', ...

    ' Original and Attenuated Noise'];

title(tstr);

legend('Original','Attenuated');

 

 

 

شکل(18-3) مقایسه طیف سیگنال خطای باقیمانده با سیگنال نویز اولیه

5-3 ANC باند فرعی

اصول کار سیستم های ANC باند فرعی، از تکنیک های پردازش وفقی باند فرعی مبتنی بر بانک فیلتری استخراج شده تا در سیستم ANC پیش خور دار برای کاربرد های متنوع استفاده شود. سیگنال ثبت شده خطای باقیمانده با استفاده از فیلتر های FIR باند گذار فاز خطی، به چند باند تقسیم می شود و الگوریتم FXLMS توصیف شده در قسمت قبل، به صورت مجزا بر روی هر یک از این باند ها پیاده سازی می شود.

 

شکل(19-3) شمای کلی یک سیستم حذف نویز باند فرعی

 

 

 پس از آن سیگنال آنتی نویز تولید شده توسط هر کدام از این بلوک ها اضافه شده و بعد از بلند گو ها پخش خواهد شد. با طراحی دقیق فیلتر های میان گذر، پهنای باند موثری که در آن نویز تضعیف می شود به طور قابل توجهی افزایش می یابد. تا زمانی که فیلتر های میان گذر دارای پهنای باند به اندازه کافی باریک باشند و طیف سیگنال را با تعداد کافی باند پوشش دهیم، می توان به تضعیف نویز تا فرکانس 4 کیلوهرتز دست یافت. با موازنه نسبت به پهنای باند افزایش یافته، در فرکانس های پایین تر، میزان اندکی کاهش در زمان همگرایی مشاهده می شود. پایداری سیستم، وابستگی زیادی به طراحی فیلتر های مورد استفاده برای جدا سازی سیگنال در باند های فرعی دارد.

6-3 شبیه سازی با استفاده از سیمولینک MATLAB

در نرم افزار MATLAB شبیه سازیهای مفیدی بصورت دمو قرار داده شده است که می توان برای سهولت کار در یادگیری و مقایسه روشهای مختلف استفاده از فیلترهای وفقی در حذف نویز آکوستیکی از آنها استفاده نمود. همچنین نمونه شبیه سازیهای مختلف الگوریتم فیلترهای وفقی که با نرم افزار MATLAB انجام شده است در اینترنت قابل جستجو می باشد. در این فصل تعدادی ازاین شبیه سازیها معرفی می شوند. همچنین بدلیل امکان ارایه نتایج بهتر توسط این شبیه سازیهاٰ، از آنها برای مقایسه کارآیی الگوریتمهای مختلف استفاده خواهیم کرد.

7-3 استفاده از سیمولینک MATLAB برای الگوریتم LMS

در این بخش دو نمونه از شبیه سازیهای انجام شده با استفاده از نرم افزار MATLAB را که برای شبیه سازی الگوریتم LMS استفاده شده است معرفی خواهیم نمود.

 

1-7-3 مدل1با استفاده از سیمولینک MATLAB برای الگوریتم LMS و NLMS

در این شبیه سازی مدل فیلتر LMS از مجموعه بلوکهای پردازش سیگنال MATLAB استفاده شده است. مدل فیلتر LMS دو ورودی دارد که به یکی از آنها سیگنال ورودی و به دیگری شکل تاخیر یافته همین سیگنال را به عنوان مرجع یا سیگنال مطلوب اعمال می کنیم. براساس این ورودیها الگوریتم فیلتر ضرایب مناسب را برای کاهش سیگنال خطا که در اینجا همان نویز محیطی است ،خواهد یافت.فایل سیمولینک MATLAB با نام AcousticNoiseCancellation.mdl از آدرس

http://www.cems.uvm.edu/~mirchand/classes/EE275/2009/Software/Shahin

قابل دانلود است. شکل 20-3 فایل اجرا شده در سیمولینک MATLAB را نشان می دهد.

 

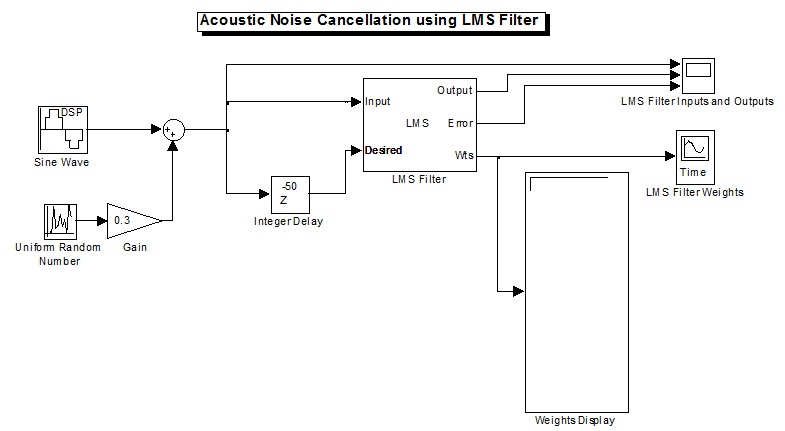
شکل(20-3) فایل اجرا شده AcousticNoiseCancellation.mdl  در سیمولینک MATLAB

 

در این مدل شبیه سازی از یک موج سینوسی دیجیتال که با اعداد تصادفی به عنوان نویز جمع شده است برای ورودی فیلتر واز شکل تاخیر یافته آن بعنوان سیگنال مرجع استفاده شده است. با اجرای شبیه سازی نمودارهای شکل 21-3 ترسیم می شوند.

 

 

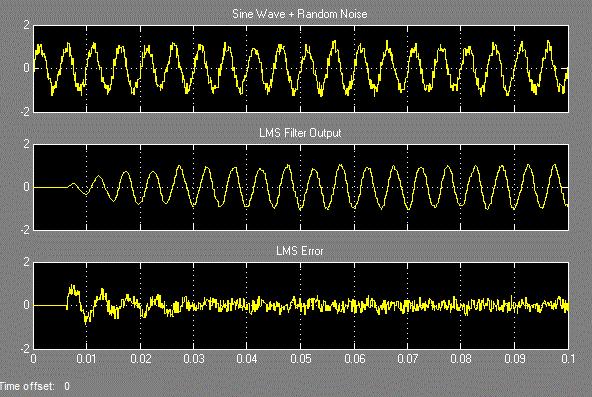
شکل (21-3) نمودارهای خروجی شبیه سازی

 

شکل 22-3 نمودار همگرایی ضرایب فیلتر LMS را نشان می دهد.

 

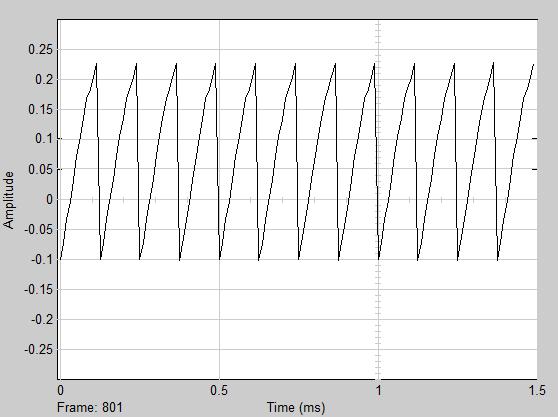
شکل(22-3) نمودار همگرایی ضرایب فیلتر LMS

 

برای استفاده از این مدل جهت شبیه سازی فیلتر نوع NLMS با دبل کلیک بر روی مدل فیلتر نوع آن را به NLMS تغییر می دهیم.

2-7-3 مدل2با استفاده از سیمولینک MATLAB برای الگوریتم LMS و NLMS

مدل دیگری که در اینجا برای شبیه سازی فیلترهای نوع LMS و NLMS معرفی می شود در قسمت  فایلهای دموی MATLAB با نام dspancموجود است. مدل ذکر شده شبیه سازی کاملی برای دو نوع فیلتر LMS و NLMS ارائه می دهد. برای بارگزاری این شبیه سازی در خط فرمان MATLABdspanc را تایپ می کنیم. شماتیک این مدل در شکل 23-3 نمایش داده شده است.

 

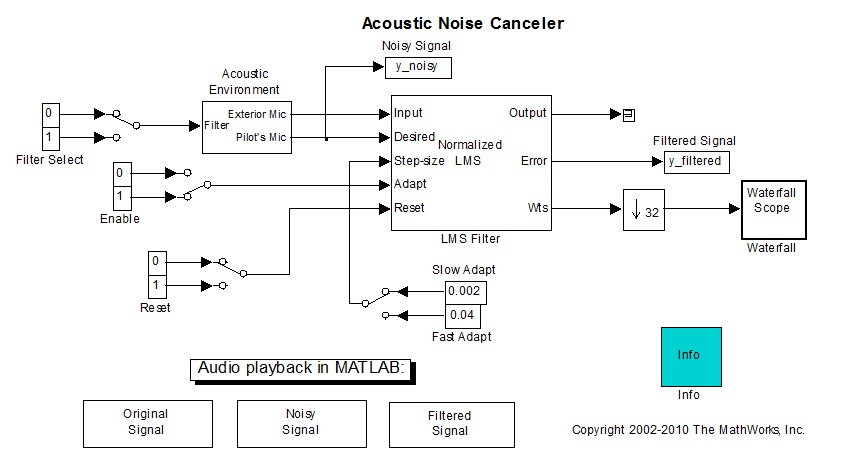
شکل(23-3) شماتیک مدل dspancموجود در برنامه MATLAB

 

در مدل شبیه سازی شده خروجی پورت بالایی بلوک Acoustic Environment نویز سفید است. خروجی پایینی مجموع یک نویز رنگی با یک سیگنال حاصل از اجرای یک فایل صوتی است..با دبل کلیک بر روی بلوک فیلتر می توان مشخصات آن را بدلخواه تنظیم نمود. با اجرای شبیه سازی بلوک Waterfall window نمودار ضرایب فیلتر را نمایش می دهد. نمونه خروجی این نمودار در شکل 24-3 نمایش داده شده است. این نمودارضرایب فیلتر را بر اساس تعداد مرتبه یا تعداد تپ  فیلتر ودر واحد زمان نشان می دهد.

 

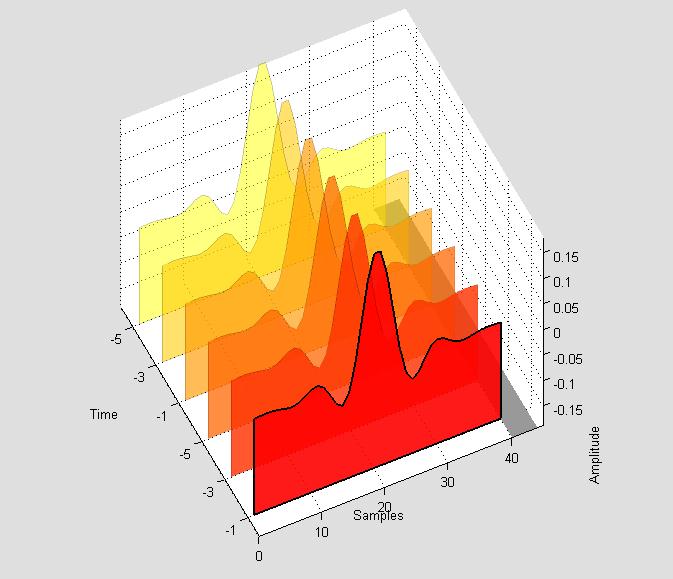
شکل (24-3) نمودار همگرایی ضرایب فیلتربر اساس مرتبه فیلتر در واحد زمان و براسا تعداد نمونه های ورودی

 

1-2-7-3 بلوک Acoustic Environment

برای تغییر فایل صوتی ویا تعریف پارامترهای مربوط به ورودیهای فیلتربا دبل کلیک برروی بلوک Acoustic Environment می توان پارامترهای مورد نظر را ویرایش نمود. از یک نویز گوسی برای خروجی Exterior Mic استفاده شده است. در صورتیکه مقدار پورت ورودی فیلتر از صفر به یک تغییر نماید، نوع فیلتر از پایین گذر به میان گذر تغییر خواهد یافت. نویز فیلتر شده خروجی از بلوک فیلتر دیجیتال با سیگنال فایل صوتی جمع شده و خروجی سیگنال به پورت Pilot's Mic را تشکیل می دهند.

 3-7-3 مدل3با استفاده از سیمولینک MATLAB برای الگوریتم LMS و NLMS

مدل دیگری که در اینجا معرفی می شود معادل مدل2 می باشد با این تفاوت که همزمان با اجرای شبیه سازی می توان پارامترهای مختلف فیلتر وسایر اجزا را تغییر داد. مدل dspanc audio در قسمت فایلهای دموی برنامه MATLAB موجود می باشد. زمان شبیه سازی در این مدل بصورت بینهایت تنظیم شده است. شکل 25-3  این مدل را نشان می دهد.

 

 

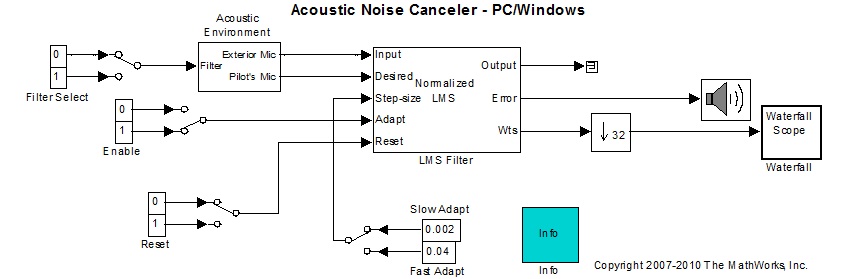
شکل (25-3) شماتیک مدل dspanc audioموجود در برنامه MATLAB

 

---

 

فصل چهارم : یافته های تحقیق

 1-4 یافته های تحقیق

برای مقایسه الگوریتمهای معرفی شده در فصل سوم ورودیهای مختلفی به هریک از الگوریتمها اعمال شده ونتایج با هم مقایسه می شوند. در ابتدا برای  شبیه سازیها نویز سفید را به عنوان ورودی در نظر می گیریم. در اولین مرحله با مشکل عدم همگرایی فیلترها مواجه شدیم که با بررسی دقیق به این نتیجه رسیدیم که بدلیل تمام باند بودن نویز سفید ضرایب وفقی هیچکدام از فیلترها همگرا    نمی شود. دلیل این امر واضح است.همانطور که در فصلهای قبل گفته شد بیشترین بازده سیستم حذف فعال نویز در فرکانسهای پایین است. برای کاهش حجم پردازش سیستمهای حذف فعال نویز عملی بایستی فرکانس نمونه برداری بهینه انتخاب شود. فرکانس انتخابی بایستی به گونه ای انتخاب شود که بتواند شرط نایکوئیست در نمونه برداری را ارضا نماید. در غیر این صورت خروجی میکروفونهای نمونه گیر و خطا بعد از دیجیتال شدن نمی توانند به عنوان مرجع مناسب به سیستم حذف فعال نویز اعمال شوند. برای حل این مشکل راه حلهای مختلفی وجود دارد که تقریبا درتمامی روشها لازم است از فیلترینگ نویز ورودی استفاده شود. یکی از راه حلهای مناسب دیگر استفاده از فیلتر آنتی فولدینگ در ورودی مبدلهای آنالوگ به دیجیتال است.علاوه بر این ترفند دیگری برای کاهش مرتبه فیلترهای ورودی وجود دارد.  در این روش بجای نرخ نمونه برداری نایکوئیست از چند برابر آن برای فرکانس نمونه برداری استفاده می شود¹ سپس تعداد نمونه ها طبق الگوریتم خاصی² کاهش داده می شود. به این ترتیب در صورتیکه از فیلترهای معمولی استفاده کنیم با مشکل Aliasing مواجه نخواهیم شد.  ابتدا با یک سینوسی تک فرکانس با مقدار µ ثابت شروع می کنیم. برای راحتی کار و داشتن یک مرجع یکسان برای تمامی الگوریتمها از مدل 1 برای شبیه سازیها استفاده می کنیم. همچنین برای مدل نویز از یک مولد اعداد تصادفی که صورت دیجیتال شده و فیلتر شده نویز سفید است استفاده می کنیم. لازم به ذکر است که دوروش FXLMS  و باند فرعی بدلیل نیاز به استفاده از مدل سخت افزاری برای اندازه گیریها قابل شبیه سازی نرم افزاری و ارائه نتایج مرجع نیستند.مگر اینکه برای الگوریتم FXLMS پاسخ ضربه مسیر ثانویه مشخص باشد و برای روش باند فرعی مشخصات کامل سیستم فیلترینگ چندباندی آورده شده باشد. برای مقایسه این دومدل با سایر انواع از نتایج مقالات ارائه شده استفاده شده است. در عین حال با توجه به اینکه اساس این دونوع فیلتر اخیر برمبنای استفاده از فیلترهای وفقی LMS و  NLMSمی باشد، نتایج شبیه سازی می تواند برای طراحی آنها استفاده شود.

 

---

1Up Sampling

2Down Sampling

 

 

 

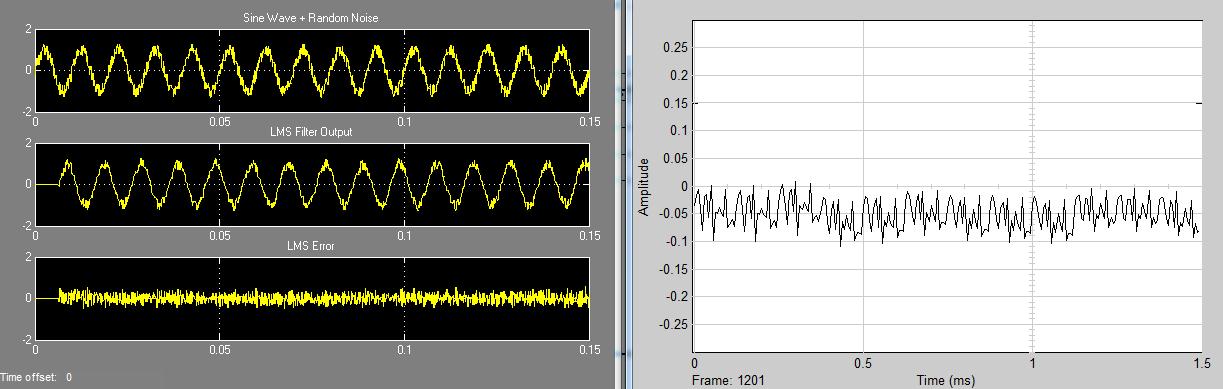
شکل(1-4) شبیه سازی نوع RLS فرکانس 100 هرتز- مرتبه 20 –µ =0.05

 

 

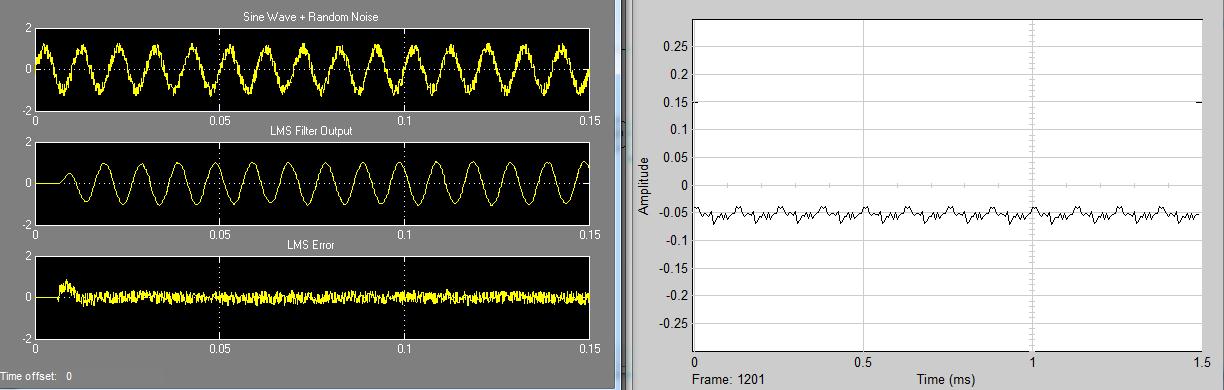
شکل(2-4) نوع LMSفرکانس 100 هرتز- مرتبه 20 –µ =0.05

 

 

شکل(3-4) نوع NLMSفرکانس 100 هرتز- مرتبه 20 –µ =0.05

 

---

 

 

فصل پنجم : نتیجه گیری

نتایج    

برای شبیه سازی الگوریتمهای LMS,NLMS,RLS  از سیمولینک MATLAB معرفی شده در فصل سوم به نام AcousticNoiseCancellation.mdl  استفاده شده است. نکته مهم دیگری که در شبیه سازیها باید در نظر گرفته شود و همچنین قبلا به آن اشاره شده است اینکه مجموع تاخیر سیستم انتقال (که در اینجا منظور تاخیر زمانی مسیر طی شده از میکروفون مرجع تا سیستم حذف فعال نویز است) بایستی از مرتبه فیلتر استفاده شده کمتر باشد. بر این اساس در تمام شبیه سازیها مجموع تاخیر انتقال یک واحد کمتر از مرتبه فیلتر در نظر گرفته شده است.  با تکرار نتایج برای تک فرکانسهای مختلف برای فیلتر از مرتبه 10تا مرتبه 50 ویا کمتر و µ از مقدار 0.1 تا مقدار 0.0001  مشاهده می شود که ضرایب فیلتر نوع LMS برای فرکانسهای پایین یعنی زیر 600 هرتزو با مقدار µ برابر0.1 و برای فیلتر مرتبه های بالا تر از 35 یا همگرا نشده ویا میزان خطای باقیمانده افزایش می یابد. با افزایش درجه فیلتر برای دو الگوریتم LMS و RLS تاثیر چندانی در همگرایی ملاحظه نمی شود. همچنین مشاهده می شود فیلتر   RLS , LMS در مقادیر µ کمتر از0.1 بهترین نوع از نظر پایداری ضرایب ودر مقابل فیلتر نوع NLMS از پایداری کمتری برخوردار است. برای ارزیابی پایداری و راندمان سیستم ANC، شبیه سازی هایی با فایل های ورودی متفاوت ( موج های سینوسی به اضافه نویز در فرکانس های مختلف در یک مرحله و مجموع دو فرکانس سینوسی با پهنای باند کمتر از یک سوم اکتاو به اضافه نویز در مرحله بعد) انجام شدند. در فرکانسهای ترکیبی از ترکیب دو فرکانس سینوسی با پهنای باند کمتر از یک سوم اکتاو استفاده شده است . دلیل این امر این است که عملا در پهنای باندهای بزرگتر ضرایب فیلتر همگرا نمی شود. از نتایج شبیه سازی چنین نتیجه می شود که برای ورودیهای تک فرکانس (فرکانس زیر 700 هرتز)فیلتر نوع LMS و RLS از لحاظ پایداری و عملکرد و زمان همگرایی ضرایب از نوع NLMS بهتر است. برای ورودیهای با پهنای باند کم (فرکانسهای زیر 700  هرتز با پهنای باند زیر یک سوم اکتاو) و µ = 0.1 عملکرد فیلتر نوع NLMS , RLS بهتر از نوع  LMSاست. از اینرو در ساخت الگوریتم حذف فعال نویز به روش باند کناری از بلوکهای فیلتری NLMS استفاده می شود. دلیل دیگر استفاده از بلوکهای فیلتری NLMS نیاز به سخت افزار کمترنسبت به نوع RLS است. از مجموع آزمایشهای انجام شده نتیجه می شود که بیشترین عامل موثر در عملکرد دو نوع فیلتر NLMS وLMS مقدار µ فیلتر است .

 

پیشنهاداتی برای فعالیتهای آینده

1.استفاده از الگوریتمهای فیلتر وفقی برای حذف اکو

2.استفاده از الگوریتمهای فیلتر وفقی برای شناسایی محل بازتاب صوتی

3.شبیه سازی سخت افزاری حذف فعال نویز

4.مکان یابی محل مناسب برای میکروفونهای نمونه گیروخطا وبلندگو یا مبدل الکتروآکوستیکی مولد سیگنال ضدنویز در یک محیط بسته

 

---

 

فهرست منابع و ماخذ

[1] P. Lueg, Process of silencing sound oscillations, U.S Patent 2,043,416, June 9,1936.

[2] S M Kuo and D.R.Morgan, Active Noise Control: a tutorial review, Proceedings of the IEEE, Volume 87, Number 6, June 1999.

[3] S M Kuo and D R Morgan, Active Noise Control Systems: algorithms and DSP implementations, John Wiley and Sons, New York, 1996.

[4] H F Olson and E G May, Electronic Sound Absorber, The Journal of the Acoustic Society of America, Volume 25, Number 6, November 1953.

[5] B Widrow and S D Stearns, Adaptive Signal Processing, Prentice-Hall, Inc.Englewood Cliffs, N.J, 1985.

[6] J C Burgess, Active adaptive sound control in a duct: A computer simulation, The Journal of the Acoustic Society of America, Volume 70, Number 3, September 1981.

[7] D R Morgan, An Analysis of Multiple Correlation Cancellation Loops with a Filter in the Auxiliary Path, IEEE Transactions of Acoustic, Speech and Signal Processing, Volume ASSP-28, Number 4, August 1980.

[8] S J Elliott and P A Nelson, Active Noise Control, IEEE Signal Processing Magazine, October 1993.

[9] C C Boucher, S J Elliott and P A Nelson, The effect of modeling errors on the performance and stability of active noise control systems, Proc. Recent Advances in Active Control of Sound Vibration, 1990, pp. 290-301.

[10] C A Jacobson, C R Johnson Jr., D C McCormick and W A Sethares, Stability of Active Noise Control lgorithms, IEEE Signal Processing Letters, Volume 8, Number 3, March 2001.

[11] J J Shynk, Adaptive IIR Filtering, IEEE ASSP Magazine, April 1989.

[12] W K W Hong, Kh. Eghtesadi and H G Leventhal, The Tight Coupled Monopole (TCM) and Tight Coupled Tandem (TCM) attenuators: Theoretical aspics and experimental attenuation in an air duct, Journal of the Acoustic Society of America, Volume 81, pp. 376-388, February 1987.

[13] I Veit, A Lightweight Headset with Active Noise Compensation, Proceedings of Inter-Noise, pp. 1087-1090, 1988.

[14] Ch Carme, A new Filtering method by Feedback for ANC at the ear, Proceedings of Inter-Noise, pp. 1083-1086, 1988.

[15] P D Wheeler and D Smeatham, On Spatial Variability in the Attenuation Performance of Active Hearing Protectors, Applied Acoustics, Elsevier Science Publishers Ltd., England, 1992.

[16] L J Eriksson, Recursive algorithms for active noise control, Proc. Int. Symp.Active Control of Sound Vib., pp. 237-245, 1991.

[17] S R Popovich, D E Melton and M C Allie, New adaptive multi-channel control systems for sound and vibration, Proc. Of Inter-Noise, pp. 405-408, 1992.

[18] S R Popovich, Multi channel active attenuation system with error signal inputs, U.S Patent 5,216,722, June 1, 1993.

[19] D Vijayan, Feedback Active Noise Control Systems, Masters thesis, Northern Illinois University, 1994.

[20] G B B Chaplin and R A Smith, Method of and apparatus for canceling vibrations from a source of repetitive vibrations, U.S Patent 4,566,118, Jan 21, 1986.

[21] A V Oppenheim, E Weinstein, K C Zangi, M Feder, D Gauger, Single Sensor Active Noise Cancellation Based on the EM Algorithm, Proc. ICASSP, Vol. I, pp.277-280, 1992.

[22] A V Oppenheim, E Weinstein, K C Zangi, M Feder, D Gauger, Single-Sensor Active Noise Cancellation, IEEE Transactions on Speech and Audio Processing, Vol. 2 No. 2, April 1994.

[23] L J Eriksson, M C Allie, D E Melton, S R Popovich, T A Laak, Fully Adaptive Generalized Recursive Control Systems for Active Acoustic Attenuation, Proc.ICASSP, Vol. II, 1994.

[24] G M Davis, Noise Reduction in Speech Applications, CRC Press, London, UK,April 2002.

[25] S M Kuo, H Chuang, P Mallela, Integrated hands-free cellular, active noise control and audio system, IEEE Transactions on Consumer Electronics, Vol. 39,pp. 522-532, August 1993.

[26] J Chaoui, S de Gregorio, G Gallisian, Y Masse, DSP-Based Solution for Ambient Noise Reduction in Mobile Phones, Proc. ICASSP, Vol. 4, 1999.

[27] D C Swanson, Active Noise attenuation using a self-tuning regulator as the adaptive control algorithm, Proc. Inter-Noise, pp. 467-470, 1989.

[28] D Graupe and A J Efron, An output-whitening approach to adaptive noise cancellation, IEEE Transactions on Circuits and Systems, Vol. 38, pp. 1306-1313,November 1991.

[29] S J Elliott, I M Stothers, P A Nelson, A M McDonald, D C Quinn, T Saunders,The active control of engine noise inside cars, Proc. Inter-Noise, pp. 987-990,1988.

[30] S M Kuo and B M Finn, A general multi-channel filtered LMS algorithm for 3-D active noise control systems, Proc. 2nd International Conference Recent Developments in Air- and Structure-Borne Sound Vibration, pp. 345-352, 1992.

[31] S J Elliott, I M Stothers, P A Nelson, A multiple error LMS Algorithm and its applications to the active control of sound and vibrations, IEEE Transactions Acoustics, Speech, Signal Processing, ASSP-35, 1423-1434, Oct. 1987.

[32] D E Melton and R A Greiner, Adaptive feedforward multiple-input, multipleoutput active noise control, Proceedings of ICASSP, Vol. II, pp. 229-232, 1992.

[33] S Laugesen and S J Elliott, Multichannel active control of sound in a reverberant room, IEEE Transactions on Signal Processing, Vol. I, 241-249, April 1993.

[34] Q Shen and A Spanias, Time and Frequency Domain X-Block LMS Algorithms for Single Channel Active Noise Control, Proc. Second International Congress on Recent Developments in Air- and Structure-Borne Sound and Vibration, pp. 353-359, March 1992.

[35] Q Shen and A Spanias, Frequency Domain Adaptive Algorithms for Multi-Channel Active Sound Control, Proc. Recent Advances in Active Control of Sound Vibration, pp. 755-766, 1993.

[36] K M Reichard and D C Swanson, Frequency domain implementation of the filtered-X algorithm with online system identification, Proc. Recent Advances in Active Sound Vibration, pp. 562-573, 1993.

[37] P F Feintuch, N J Bershad and A K Lo, A frequency domain model for “filtered” LMS algorithms – stability analysis, design and elimination of the training mode,IEEE Transactions on Signal Processing, Vol. 41, pp. 1518-1531, April 1993.

[38] J J Shynk, Frequency Domain and multirate adaptive filtering, IEEE Signal Processing Magazine, Vol 9, pp. 14-37, Jan 1992.

[39] D R Morgan and J C Thi, A Delayless Subband Adaptive Filter Architecture, IEEE Transactions on Signal Processing, Vol. 43, No. 8, August 1995.

[40] J C Thi and D R Morgan, Delayless Subband Active Noise Control, Proc.ICASSP, Vol. 1, pp. 181-184, 1993.

70

[41] S J Park, J H Yun, Y C Park D H Youn, A Delayless Subband Active Noise Control System for Wideband Noise Control, IEEE Transactions on Speech and Audio Processing, Vol. 9, No. 8, November 2001.

[42] A Hussain and D R Campbell, Intelligibility improvements using binaural diverse sub-band processing applied to speech corrupted with automobile noise, IEEE Proc. Visual Image Signal Processing, Vol. 148, No.2, April 2001.

[43] A Gilloire and M Vetterli, Adaptive Filtering in sub-bands, Proc. ICASSP, Vol. 3, pp. 1572-1575, 1988.

[44] B E Usevitch and M T Orchard, Adaptive Filtering using Filter Banks, IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing,Vol. 43, No. 3, March 1996.

[45] M R Petraglia and R G Alves, New Results on Adaptive Filtering Using Filter Banks, IEEE International Symposium on Circuits and Systems, 1997.

[46] R G Alves, M R Petraglia and P S R Diniz, Convergence Analysis of an Oversampled Subband Adaptive Filtering Structure Using Global Error, Proc.ICASSP, Vol. 1, pp. 468-471, 2000.

[47] Texas Instruments Inc., DHP Hearing Development Kit for DHP 100 Users Guide, SPRU551, September 2001.

[48] T E Quatieri, Discrete time speech signal processing – principles and practices,Prentice Hall, N J, October 2001.

[49] J F Kaiser, On a simple algorithm to calculate the “energy” of a signal, Proc.ICASSP, Vol. 1, pp. 381-384, 1990.

[50] Kuo S.M. and Morgan D.R.Active Noise Control Systems Algorithms and DSPImplementations. New York, John Wiley & Sons, Inc. 1996.

[51] Hansen C.H. Understanding Active Noise Cancellation. London, Spon Press,2001.

 

---

 

پیوست

  پیوست الف

1- الف حذف نویز وفقی ( ANC ) مورد استفاده در الکتروکاردیوگرافی جنینی

در این مثال، کاربرد فیلتر های وفقی برای حذف نویز با استفاده از ANC نشان داده می شود. در حذف نویز وفقی، یک سیگنال اندازه گیری شده شامل دو سیگنال (یک سیگنال مطلوب نامشخص v(n) و یک سیگنال تداخلی u(n)) می باشد. هدف این الگوریتم، جداسازی و حذف سیگنال تداخلی از سیگنال اندازه گیری شده، با استفاده از یک سیگنال مرجع x(n) (که شدیدا با سیگنال تداخلی همبسته است)، می باشد. مثالی که در اینجا بیان می شود کاربردی از فیلتر های وفقی برای الکتروکاردیوگرافی  جنین است که در آن سیگنال تپش قلب مادر به صورت وفقی از سیگنال تپش قلب جنین جدا می شود. این روش برگرفته از مقاله زیر می باشد.

 

Widrow, et al, ”Adaptive noise canceling:Principles and applications,” Proc. IEEE, vol. 63, no. 12, pp. 1692-1716,December 1975.

1-1- الف تولید سیگنال تپش قلب مادر

 

در این مثال باید شکل الکتروکاردیوگرام را هم برای مادر و هم برای جنین شبیه سازی کنیم. دستورات زیر می توانند یک سیگنال الکتروکاردیوگرام که قلب مادر با فرض نرخ نمونه برداری 4000 هرتز تولید می- کند، را بسازند. برای این سیگنال، نرخ تپش قلب تقریبا برابر 89 ضربان در دقیقه می باشد و ولتاژ پیک سیگنال برابر 3/5 میلی ولت است.

 

x1 = 3.5*ecg(2700).';

y1 = sgolayfilt(kron(ones(1,13),x1),0,21);

n = 1:30000;

del = round(2700*rand(1));

mhb = y1(n + del);

t = 0.00025:0.00025:7.5;

plot(t,mhb);

axis([0 2.5 -4 4]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Maternal Heartbeat Signal');

 

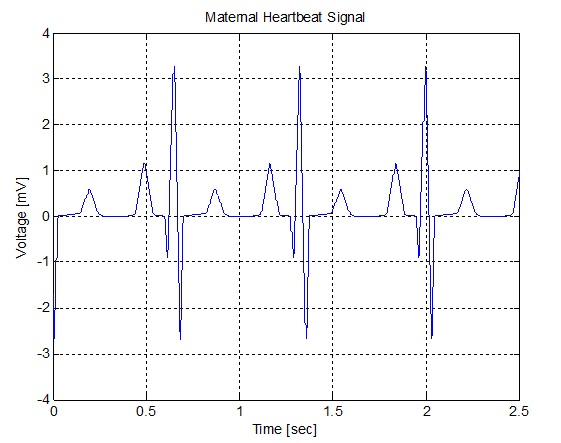
شکل(الف-1) سیگنال ضربان قلب مادر

2-1- الف تولید سیگنال تپش قلب جنین

 

سرعت ضربان قلب جنین به طور قابل توجهی از سرعت تپش قلب مادر بیشتر است و در محدوده 120 تا 160 مرتبه در دقیقه قرار دارد. دامنه الکتروکاردیوگرام جنین نیز از الکتروکاردیوگرام مادر خیلی ضعیف تر است.  دستورات زیر می توانند سیگنال الکتروکاردیوگرام با سرعت ضربان 139 تپش در دقیقه و ولتاژ پیک 0.25 میلی ولت را بسازند.

 

x2 = 0.25*ecg(1725);

y2 = sgolayfilt(kron(ones(1,20),x2),0,17);

del = round(1725*rand(1));

fhb = y2(n + del);

plot(t,fhb);

axis([0 2.5 -1 1]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Fetal Heartbeat Signal');

 

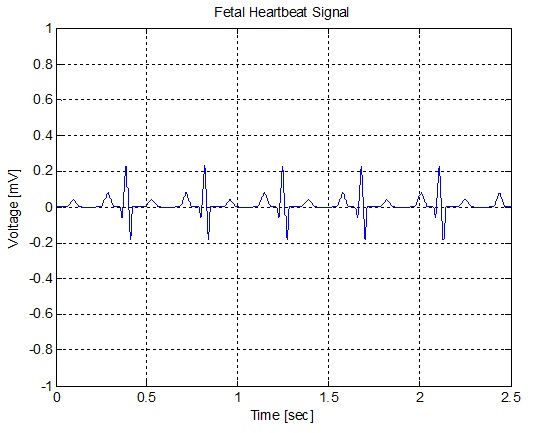
شکل(الف-2) سیگنال ضربان قلب جنین

 

3-1- الف الکتروکاردیوگرام اندازه گیری شده جنین

 

سیگنال الکتروکاردیوگرام جنین اندازه گیری شده از شکم مادر، معمولا تحت تاثیر سیگنال ضربان قلب مادر که از قفسه سینه تا شکم منتشر می شود، قرار دارد. ما باید این مسیر انتشار را به عنوان یک فیلتر FIR خطی با 10 ضریب تصادفی، توصیف کنیم. به علاوه برای در نظر گرفتن و شبیه سازی هر گونه نویز پهن باند ناشی از منبع خارجی  باید مقدار اندکی نویز گوسی ناهمبسته را به آن اضافه کنیم. آیا می توانید با دیدن این سیگنال اندازه گیری شده، نرخ ضربان قلب جنین را تعیین کنید.

 

Wopt = [0 1.0 -0.5 -0.8 1.0  -0.1 0.2 -0.3 0.6 0.1];

d = filter(Wopt,1,mhb) + fhb + 0.02*randn(size(mhb));

plot(t,d);

axis([0 2.5 -4 4]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Measured Signal');

 

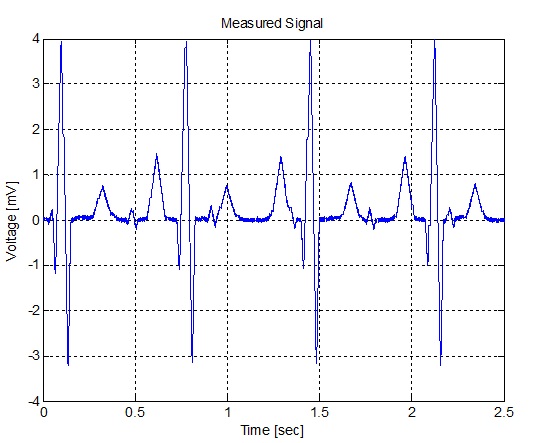
شکل(الف-3) الکتروکاردیوگرام اندازه گیری شده جنین

 

4-1- الف الکتروکاردیوگرام اندازه گیری شده مادر

 

 سیگنال الکتروکاردیوگرام مادر از قفسه سینه بدست می آید. هدف از حذف نویز وفقی این است که سیگنال ضربان قلب مادررا به صورت وفقی از سیگنال الکتروکاردیوگرام جنین جدا کنیم. برای حذف نویز به یک سیگنال مرجع نیاز است که از الکتروکاردیوگرام مادر تولید شده باشد. سیگنال الکتروکاردیوگرام مادر نیز مانند سیگنال الکتروکاردیوگرام جنین حاوی مقداری نویز پهن باند اضافی نیز هست.

 

x = mhb + 0.02*randn(size(mhb));

plot(t,x);

axis([0 2.5 -4 4]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Reference Signal');

 

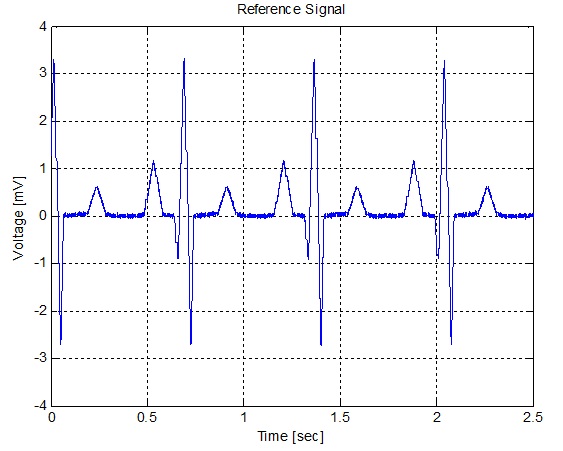
شکل(الف-4) الکتروکاردیوگرام اندازه گیری شده مادر

 

5-1- الف پیاده سازی ANC

 

می توان برای پیاده سازی ANC از هر روال وفقی استفاده کرد . برای ساده سازی باید از فیلتر وفقی LMS (حداقل میانگین مربع ) با 15 ضریب و اندازه گام 0.00007 استفاده کرد. با این تنظیمات فرآیند حذف نویز با همگرا شدن وزنهای فیلتر وفقی، در زمان معقول  وتنها پس از چند ثانیه، به حدقابل قبول خواهد رسید.

 

h = adaptfilt.lms(15,0.00007);

[y,e] = filter(h,x,d);

plot(t,d,'b',t,e,'r');

axis([0 7 -4 4]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Convergence of Adaptive Noise Canceler');

legend('Measured Signal','Error Signal');

 

 

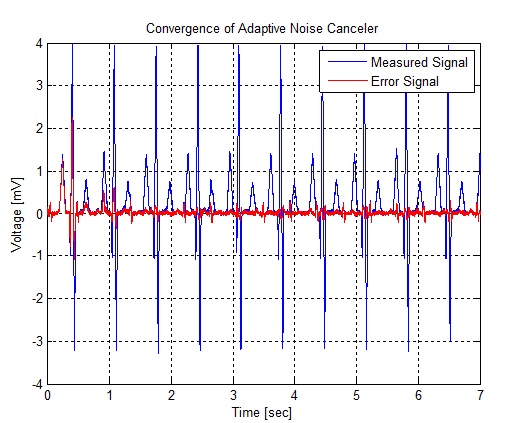
شکل(الف-5) نمودار عملکردفیلتر وفقی در حذف نویز (سیگنال ضربان قلب مادر)وزمان همگرایی ریشه های فیلتر

6-1- الف آشکارسازی ضربان قلب جنین

 

سیگنال y(n) خروجی از فیلتر وفقی، شامل سیگنال ضربان قلب مادر نیز می باشد که نمی تواند به عنوان خروجی قابل قبول استفاده شود. سیگنال خطای باقیمانده پس از همگرایی ضرایب فیلتر، شامل صدای ضربان قلب جنین و باقیمانده نویز است که سطح نویز باقیمانده خیلی کم و صدای قلب جنین کاملا قابل تشخیص است .

 

plot(t,e,'r');

axis([6 7.5 -0.5 0.5]);

grid;

xlabel('Time [sec]');

ylabel('Voltage [mV]');

title('Steady-State Error Signal');

 

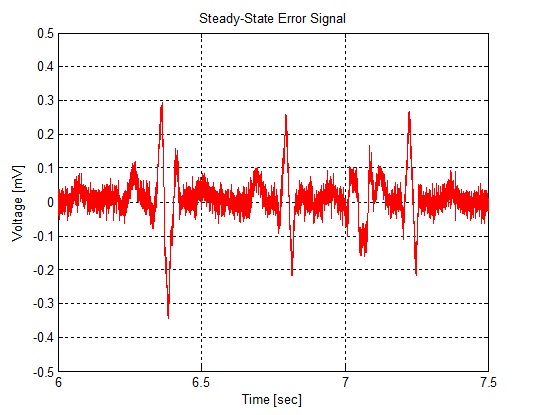
شکل(الف-6) نمودار سیگنال خطا

 

 

---